反向传播补充

1. 反向传播的直观理解

反向传播是一个高度本地化(local)的过程，可以看作是电路中各个“门”（gate）之间的通信：

$a.$ 本地化

电路中的每一个“门”（比如一个加法门、一个乘法门）在工作时，完全不需要知道整个电路有多复杂，也不需要知道自己处在电路的哪个位置。它是一个独立的、封装好的模块，只会完成自己对应的操作。

在神经网络中，这部分表现如下：

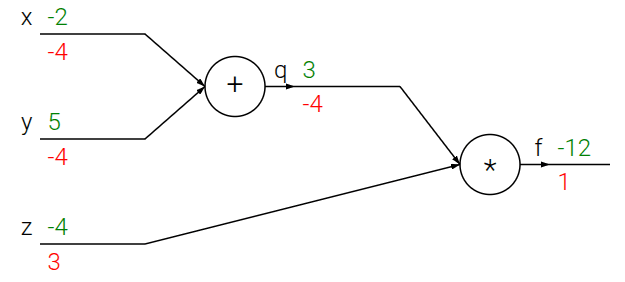
1. 计算输出值（前向传播）：给它输入，它就算出输出。例如，加法门输入 $[-2, 5]$，它就输出 3。
2. 计算局部梯度（为反向传播做准备）：它还需要知道输出相对于其输入的局部梯度（local gradient）。这个梯度只描述了“门”自己的特性。
   • 加法门 ($z = x + y$)：$∂z/∂x = 1, ∂z/∂y = 1$。它的局部梯度永远是 1。
   • 乘法门 ($z = xy$)：$∂z/∂x = y, ∂z/∂y = x$。它的局部梯度是另一个输入的值。

这一过程完全是独立的。

$b.$ 链式法则

那么既然每个门是独立的，它们之间怎么进行信息传递呢？链式法则就承担了这一角色。

在反向传播时，每个门会从它的“下游”（靠近最终输出的方向）接收到一个梯度值。这个值，称为上游梯度（upstream gradient）或全局梯度（global gradient）。它代表了整个电路的最终输出对当前这个门输出的梯度。这个梯度告诉门：“你的输出值对最终结果有多大的影响。”

而链式法则本质上是进行如下的计算：全局梯度 = 上游梯度 $\times$ 局部梯度。这个计算出的梯度就是新的下游梯度。然后这个梯度会传播给它的上游。

通过链式法则，独立的门就变成了复杂系统紧密协作的一环。

$c.$ 总结

反向传播本质上是一个通信协议，其中：

• 梯度就是信号。
• 信号的内容是：告诉每一个门，它们应该增加还是减少自己的输出值（由梯度的正负号决定），以及这种调整的迫切程度（由梯度的大小决定）。
• 最终的目的是：服务于一个全局目标——让整个电路的最终输出值最大化（或者在机器学习中，让损失函数最小化）。

2. 反向传播的模块化

$a.$ 门的视角

神经网络中的“门”的定义是灵活的，任何可微分的函数都可以被看作一个“门”，我们可以把多个小门组合成一个大门，也可以把一个复杂函数分解成多个小门。

以下面的例子为例：

$b.$ 分解视角

我们可以将这个函数分解成下面的门：

• $mul$
• $add$
• 四个新引入的一元门：$\frac{1}{x}$, $c+x$, $e^x$, $ax$

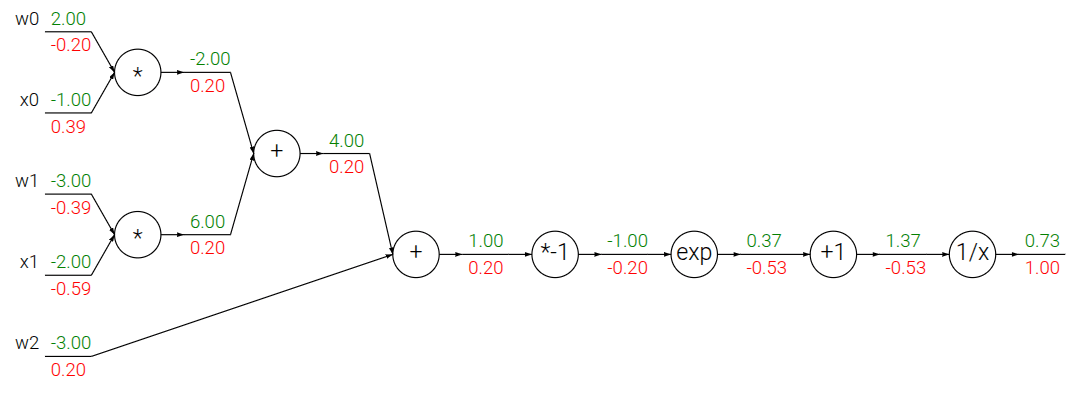
$c.$ 组合视角

我们考虑 Sigmoid 函数 $\sigma(x)$，它的导数可以简单的用自身表示：$\frac{d\sigma(x)}{dx}=(1-\sigma(x))\sigma(x)$。

因此，我们不再需要关心 Sigmoid 内部的四个步骤，而是可以把它看作一个单一的、原子的“Sigmoid门”。

$d.$ 分阶段反向传播

下面是基于组合视角与分阶段实现思想的代码实现：

w = [2,-3,-3] # assume some random weights and data
x = [-1, -2]

# forward pass
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid function

# backward pass through the neuron (backpropagation)
ddot = (1 - f) * f # gradient on dot variable, using the sigmoid gradient derivation
dx = [w[0] * ddot, w[1] * ddot] # backprop into x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # backprop into w
# we're done! we have the gradients on the inputs to the circuit

1. 前向传播：
   • 第一阶段：计算点积 $dot = w[0]x[0] + w[1]x[1] + w[2]$。这里把三个乘法和两个加法组合成一个“点积门”。
   • 第二阶段：计算 $f = 1.0 / (1 + math.exp(-dot))$。这里把四个基础门组合成一个“Sigmoid门”。
2. 反向传播：
   • 第一阶段 (逆序)：计算 $f$ 对 $dot$ 的梯度。我们直接使用 $ddot = (1 - f) * f$ 这个简洁的公式，完全不用关心 Sigmoid 内部的细节。
   • 第二阶段 (逆序)：计算 $dot$ 对 $w$ 和 $x$ 的梯度。我们把 $ddot$ 作为上游梯度，乘以点积门的局部梯度。

注意，不要试图一步到位地计算出最终梯度，而是应该像搭积木一样，将复杂的计算过程分解成一系列简单的、可管理的“阶段”或“模块”。

这个过程就像一个“计算栈”：前向传播每完成一个阶段的计算，就把结果（比如 dot）和它的计算方式压入栈中。反向传播从栈顶开始，一步步地弹出每个阶段，并计算其对应的梯度，直到栈被清空。

从这个例子我们也可以看出划分门的方法：

1. 寻找“梯度友好”的边界：在设计网络或写代码时，要有意识地去识别那些具有简洁梯度表达式的函数块（比如 Sigmoid, ReLU等）。
2. 封装成层 ：将这些函数块封装成一个“层”或“模块”。这个层对外暴露一个简单的前向接口和一个简单的反向接口。

3. 反向传播中的一般规律

$a.$ 基本门的梯度行为

• 加法门是梯度的 “分发器” (Distributor)，会把从下游传来的“上游梯度”，原封不动、均等地分配给它的所有输入。
  • 这是因为加法操作 $f(x, y) = x + y$ 的局部梯度 $∂f/∂x$ 和 $∂f/∂y$ 永远是 1。根据链式法则，下游梯度 $L$ 乘以局部梯度 1，结果还是 $L$。
• 最大值门是梯度的 “路由器” (Router)，会把上游梯度完整地、只传递给那个在前向传播中值最大的输入，而其他所有输入的梯度都为0。
• 乘法门是梯度的梯度的 “交换缩放器” (Swapper & Scaler)，会接收上游梯度，然后把它分别乘以另一个输入的值，再传递给对应的输入。
  • 这是因为对于 $f(x, y) = xy$，局部梯度是 $∂f/∂x = y$ 和 $∂f/∂y = x$。梯度被“交换”了。
  • 可以这样理解：每个输入对输出的贡献，是由另一个输入的值来“放大”或“缩小”的。所以反向传播时，梯度的大小也由另一个输入的值来决定。