依存句法分析中的增量性

1.相关概念

在最严格的意义上，增量性指的是：在句法分析的任何一个时间点，对于已经处理过的输入部分，我们都能得到一个单一的、连通的结构来表示其分析结果。

2.基本依存句法分析的缺陷

$a.$ 算法回顾

最基本的基于依存句法的分析包含移入 (Shift)、左向规约 (Left-Reduce) 和 右向规约 (Right-Reduce)三个基本动作：

• 左向规约：处理栈最顶端的两个词 $w_i$ 和 $w_j$。它会创建一个依存关系，让顶端的词 $w_j$ 成为中心语，而它下面的词 $w_i$ 成为依存词。这条依存弧是“左向”的，因为依存词 $w_i$ 在句子中的位置在中心语 $w_j$ 的左边。创建完 $w_j \rightarrow w_i$ 这条弧后，作为依存词的 $w_i$ 就从栈上被移除。
• 右向规约：同样处理栈最顶端的两个词 $w_i$ 和 $w_j$。它创建的依存关系是让下面的词 $w_i$ 成为中心语，而顶端的词 $w_j$ 成为依存词。这条弧是“右向”的，因为依存词 $w_j$ 在句子中的位置在中心语 $w_i$ 的右边。创建完 $w_i \rightarrow w_j$ 这条弧后，作为依存词的 $w_j$ 就从栈上被移除。
• 移入：从缓冲区的开头取下一个词，然后把它放到栈的最顶端。

在最基本的依存句法分析框架下，增量性可以转换成如下的规范：在任何时候，栈的大小都不超过2。这一要求强制规定：每当我们要移入第三个词时，必须先处理掉栈上的前两个词，通过左规约或右规约把它们连接起来，为新来的词腾出空间。这个约束迫使分析器在看到新信息后，立刻对已有的信息进行整合，是增量处理思想的体现。

$b.$ 算法在严格增量性上的反例

上面这种简单的依存句法分析算法是不满足严格增量性的。例如下面几个反例：

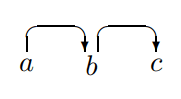
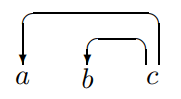
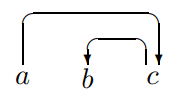
这些反例揭示了简单算法的如下的问题：

1. 我们的算法有一个最基本的规则——任何规约操作都必须在两个词之间建立直接的中心语-依存词关系。因此当栈中的两个词语并非中心词-依存语关系时，我们就无法进行规约操作了，而进行 Shift 操作又导致栈的大小超过了2，违背了严格增量性。
2. 然后我们的算法又有如下的策略：一个词必须先找到它自己所有的依存词，然后才能连接到它自己的中心语。但当一个结构是右分支结构（$c\rightarrow b \rightarrow a$）时，中间的词语 $b$ 由于没有处理完自己的依存词，无法与 $a$ 构建规约关系。

对于这些问题，只需要修改一下现有的分析策略即可。

3. Arc-Eager算法

$a.$ 算法描述

Arc-Eager 算法有自己的一套新动作。一个关键区别是：这些动作主要在栈顶的词和输入缓冲区的第一个词之间进行，而不是在栈顶的两个词之间：

1. 左弧：在输入缓冲区的下一个词 $w_j$ 和栈顶的词 $w_i$ 之间，建立一条 $w_j \rightarrow w_i$ 的弧（即 $w_j$ 是中心语）。
   • 建立弧之后，将栈顶的词 $w_i$ 弹出。因为它已经找到了自己的父亲，任务完成了。
2. 右弧：在栈顶的词 $w_i$ 和输入缓冲区的下一个词 $w_j$ 之间，建立一条 $w_i \rightarrow w_j$ 的弧（即 $w_i$ 是中心语）。
   • 建立弧之后，将输入词 $w_j$ 压入栈中。这是关键！$w_j$ 虽然找到了自己的父亲 $w_i$，但它自己可能还有孩子，所以它要进入栈中，继续寻找自己的孩子。
3. 规约：将栈顶的词弹出。
   • 只有当栈顶的词已经找到了它的中心语时，才能执行此操作。它的作用是移除一个已经处理完毕（既找到了父亲，也找到了所有孩子）的词。
4. 移入：将输入缓冲区的下一个词压入栈中。
   • 和之前一样，这是在无法进行任何“建弧”或“规约”操作时的默认选择，用于将新词纳入考虑。

这个新的算法的决策方法更加的灵活，避免了前面的简单算法在增量性上的问题。

$b.$ 新算法的增量性

因为在 Arc-Eager 算法中，栈里可以合法地包含一长串已经连接好的词。所以，一个大的栈不再意味着“拖延”，而是可能意味着正在处理一个复杂的、连接的结构。

对于新算法，我们定义新的增量性规范：在任何时候，由当前栈中所有的词 $S$ 以及这些词之间已经建立的依存弧 $AS$ 所构成的那个子图，必须是连通的。

这个定义更本质地抓住了“增量”的含义——每一步处理都在一个已连接的结构上进行扩展。

需要注意，上面最后两种结构依然无法被增量分析。计算语言学中一个众所周知的结论是：纯粹的自底向上分析器在处理右分支结构时，可能需要无限大的内存空间。这从一个更根本的理论层面解释了为什么这些结构如此难以处理。