本地搜索

1. 相关概念

$a.$本地搜索概念

在某些问题中，我们只关心找到目标状态而并不需要知道达到这个状态的优化路径，并不需要通过设计算法来让路径成本优化。局部搜索算法允许我们找到目标状态而无需优化到达那里的路径成本。

在局部搜索问题中，状态空间由“完整”解的集合组成。我们使用这些算法来尝试找到满足某些约束或优化某个目标函数的配置。

局部搜索算法的基本思想是，从每个状态出发，它们局部地向具有更高目标值的状态移动，直到达到一个最大值（期望是全局最大值）。

$b.$状态空间景观

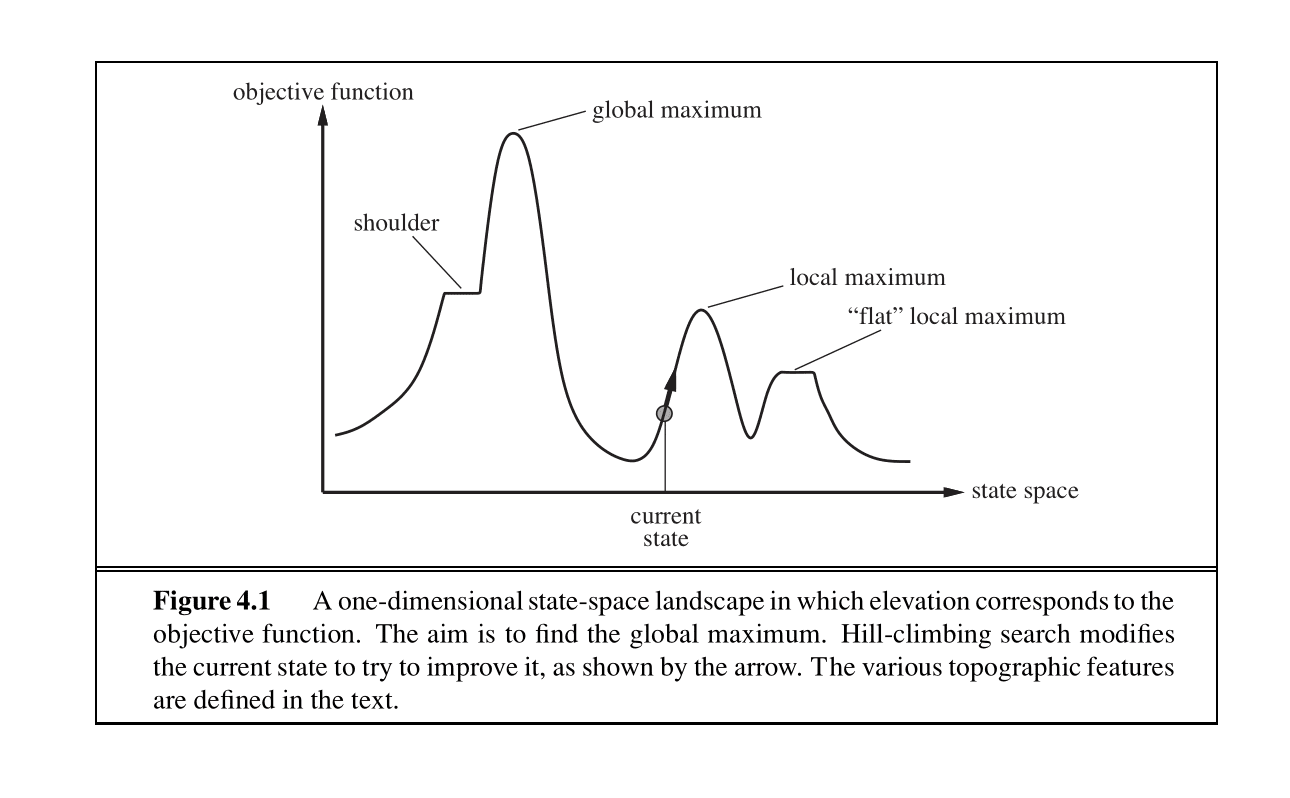
状态空间景观代表了在整个状态空间中，每个状态对应的目标函数值：

• Global Maximum (全局最大值): 这是整个“景观”中的最高点。它代表了问题的最优解。所有搜索算法的最终目标就是找到这个点。
• Local Maximum (局部最大值): 这是一个“山峰”，它比其紧邻的区域要高，但并非整个景观的最高点。简单的搜索算法很容易陷入局部最大值，以为找到了最优解，但实际上并非如此。
• "Flat" Local Maximum (平坦局部最大值): 这是一片平坦的高地（高原），上面的所有点的值都相同，并且都比周围的点要高。算法到达这里后，因为周围没有比当前位置更高的点，所以可能会停止搜索，从而被困住。
• Shoulder (山肩): 这是一片平坦的区域，但它位于通往更高山峰的路上。算法走到这里时，可能会因为短时间内看不到值的提升而提前终止，无法继续“爬”向真正的山峰。
• Current State (当前状态): 表示算法当前所在的位置。图中的箭头指示了算法的下一步移动方向——总是朝着目标函数值更高的方向移动。

2. 爬山搜索

$a.$相关概念

爬山搜索算法从当前状态向能够最大程度增加目标值的邻近状态移动。该算法不维护搜索树，只跟踪状态和目标函数的相应值。

爬山法的贪心策略使其容易出现在状态空间景观中的问题。

$b.$简单实现

我们承接有信息搜索中定义的数据结构来实现爬山算法。我们复用启发式算法中的启发函数h来衡量当前的状态，即：路径成本越高、状态越“低”。然后每次都选择状态最“高”的节点进行拓展：

def hill_climbing(problem):
    # initial node
    current_node = Node(problem.initial_state)
    
    while True:
        # find the successor with the 'highest' state
        successors = list(expand(problem, current_node))

        if not successors:
            return current_node
        
        best_successor = min(successors, key=lambda node: problem.h(node.state))

        # judge if the state gets higher
        if problem.h(best_successor.state) >= problem.h(current_node.state):
            return current_node
        current_node = best_successor

3. 模拟退火搜索

$a.$相关概念

由于爬山算法很容易得出错误的最优状态，我们引入随机游走，让搜索更有效率与完整。在模拟退火中，我们允许向可能降低目标值的状态移动。

模拟退火算法在每个时间步选择一个随机移动。

• 如果移动导致更高的目标值，移动被接受。
• 如果移动导致更小的目标值，该移动以一定的概率被接受。这个概率由温度参数决定，该参数初始值很高（允许更多“坏”的移动），并根据某个“调度”逐渐降低。

理论上，如果温度降低得足够慢，模拟退火算法将以接近1的概率达到全局最大值。

证明过程需要用到马尔科夫链和吉布斯分布，这里略去。

$b.$简单实现

实现模拟退火算法，只需要设计调度函数，然后根据当前温度执行随机游走即可：

def schedule(t, T0=100, alpha=0.95):
    """a simple exponential decay schedule for temperature."""
    if t <= 0:
        return T0
    return T0 * (alpha ** t)

def simulated_annealing(problem, schedule_func=schedule):
    current_state = problem.initial_state

    # the loop runs for a fixed number of iterations (t).
    for t in range(1, 5000):
        # get the current temperature T from the schedule.
        T = schedule_func(t)

        # if temperature is effectively zero, we stop.
        if T < 1e-4:
            return Node(state=current_state)

        # Choose a random action to find a "randomly selected successor".
        action = random.choice(possible_actions)
        next_state = problem.result(current_state, action)
        
        # Calculate the change in "value" or "energy".
        # We are minimizing h(n), so a lower h is better.
        # ΔE = h(current) - h(next). A positive ΔE means the next state is better.
        delta_E = problem.h(current_state) - problem.h(next_state)
        
        if delta_E > 0:
            # The new state is better, so we move to it.
            current_state = next_state
        else:
            # The new state is worse.
            # We might still move to it with a probability of e^(ΔE/T).
            # Since ΔE is negative or zero, this probability is between 0 and 1.
            if random.random() < math.exp(delta_E / T):
                current_state = next_state
    
    return Node(state=current_state)

4. 局部束搜索

$a.$相关概念

局部束搜索是爬山搜索算法的另一个变体。局部束搜索在每次迭代中跟踪$k$个状态（线程）。算法以$k$个状态的随机初始化开始，在每次迭代中，它从所有线程的后继状态的完整列表中选择$k$个最佳的后继状态。如果任何线程找到了最优值，算法就停止。

$k$个线程可以相互共享信息，允许“好”的线程“吸引”其他线程到那个区域。

$b.$简单实现

我们在原有的Problem中引入random_state方法：

class Problem():
    ...
    @abstractmethod
    def random_state(self):
        """生成一个随机状态"""
        pass

def local_beam_search(problem, beam_width=3):
    # Start with k randomly generated states
    current_nodes = [Node(problem.random_state()) for _ in range(beam_width)]

    while True:
        all_successors = []
        # Generate all successors for all nodes in the current beam
        for node in current_nodes:
            successors = list(expand(problem, node))
            all_successors.extend(successors)

        if not all_successors:
            # No more successors, return the best node found so far
            best_node = min(current_nodes, key=lambda n: problem.h(n.state))
            return best_node, expanded_nodes

        # Sort all successors by their heuristic value (lower is better)
        all_successors.sort(key=lambda node: problem.h(node.state))

        # Select the best `beam_width` successors for the next generation
        next_nodes = all_successors[:beam_width]

        # If the best successor is not better than the best current node, we might be at a local minimum
        best_current_h = problem.h(min(current_nodes, key=lambda n: problem.h(n.state)).state)
        best_next_h = problem.h(next_nodes[0].state)

        if best_next_h >= best_current_h:
            # Return the best node found so far
            best_node = min(current_nodes, key=lambda n: problem.h(n.state))
            return best_node

        current_nodes = next_nodes

5. 遗传搜索

$a.$相关概念

遗传算法是局部束搜索的一个变体，它以$k$个随机初始化的状态（称为种群）开始，通过模拟选择（Selection）、交叉和变异等遗传学操作，每一代种群都会进化，产生出越来越好的解，最终逼近问题的最优解。相关概念如下：

• 个体 (Individual)：表示问题的一个潜在解，也常被称为染色体(Chromosome)。
• 基因 (Gene)：构成个体的基本单元。一个染色体由多个基因组成，每个基因代表解的一个参数或特征。通常用二进制串、浮点数或整数来编码。
• 种群 (Population)：由多个个体组成的集合。
• 适应度函数 (Fitness Function)：用于评估一个个体（即一个解）的优劣程度的函数。适应度越高的个体，代表它是一个越好的解。这是算法“选择”操作的依据。
• 遗传操作 (Genetic Operators)：
  • 选择 (Selection)：根据适应度从当前种群中选择“优秀”的个体，用于繁殖下一代。适应度高的个体被选中的概率更大。
  • 交叉 (Crossover)：模拟生物的交配。从父代个体中选取两个，交换它们的部分基因，从而产生新的子代个体。这是产生新解的主要方式。
  • 变异 (Mutation)：模拟基因的突变。以一个很小的概率随机改变个体中的某个或某些基因。这有助于维持种群的多样性，防止算法过早收敛到局部最优解。

$b.$简单实现

$i.$函数设计

def genetic_algorithm(
    population, 
    fitness_fn, 
    gene_pool,
    max_generations=1000, 
    mutation_rate=0.01, 
    fitness_threshold=None
):
    """
    Implements a genetic algorithm based on the pseudocode from the image.

    Args:
        population (list): The initial population of individuals.
        fitness_fn (function): A function that takes an individual and returns its fitness score.
        gene_pool (list or string): The set of possible values for each gene.
        max_generations (int): The maximum number of generations to run.
        mutation_rate (float): The probability of a mutation occurring in a child.
        fitness_threshold (float): If the best fitness reaches this value, the algorithm stops.
    Returns:
        The best individual found.
    """

$ii.$遗传操作

def genetic_algorithm(...):
    
    def reproduce(x, y):
        """Reproduces a child from two parents using single-point crossover."""
        n = len(x)
        if n == 0:
            return ""
        c = random.randint(0, n - 1)
        return x[:c] + y[c:]
    
    def mutate(child):
        """Mutates a single gene in the child's chromosome."""
        if not child:
            return child
        index_to_mutate = random.randint(0, len(child) - 1)
        new_gene = random.choice(gene_pool)
        mutated_child = list(child)
        mutated_child[index_to_mutate] = new_gene
        return "".join(mutated_child)

$iii.$个体选择

def genetic_algorithm(...):

    def random_selection(population, fitness_fn):
        """
        Selects an individual from the population using fitness-proportionate selection (roulette wheel).
        """

        # Calculate fitness scores for all individuals
        fitness_scores = [fitness_fn(individual) for individual in population]
        total_fitness = sum(fitness_scores)

        # Handle the case where total fitness is zero to avoid division by zero
        if total_fitness == 0:
            return random.choice(population)
        
        # Pick a random value 
        # We choose the individual that first exceed the value
        pick = random.uniform(0, total_fitness)
        current = 0
        for i, individual in enumerate(population):
            current += fitness_scores[i]
            if current > pick:
                return individual
        
        # Fallback in case of floating point issues
        return population[-1]

$iv.$遗传算法实现

def genetic_algorithm(...):
    for generation in range(max_generations):
        # Calculate fitness of the current population
        fitness_scores = [fitness_fn(individual) for individual in population]
        best_fitness = max(fitness_scores)
        best_individual = population[fixness_scores.index(best_fitness)]

        # Check for stopping condition
        if fitness_threshold is not None and best_fitness >= fitness_threshold:
            print("Fitness threshold reached!")
            return best_individual

        new_population = []

        # Generate new population
        # We should ensure that both new and old population are in the same size 
        for _ in range(len(population)):
            x = random_selection(population, fitness_fn)
            y = random_selection(population, fitness_fn)

            # Parents generate new population
            child = reproduce(x, y)
            if random.random() < mutation_rate:
                child = mutate(child)
            new_population.append(child)

        population = new_population

    # Return the best individual from the final population
    fitness_scores = [fitness_fn(individual) for individual in population]
    best_fitness = max(fitness_scores)
    best_individual = population[fitness_scores.index(best_fitness)]
    print("Maximum generations reached.")
    return best_individual