Minimax 算法

1. Minimax 核心思想

Minimax（极小化极大）是一种在零和博弈中做出决策的经典算法。其核心思想是，在一个回合制、信息完全的对抗游戏中，我方（MAX玩家）总是希望最大化自己的收益，而对手（MIN玩家）则总是希望最小化我方的收益。算法假定对手每一步都会做出最优选择。

$a.$ 状态值

一个状态的值 (Value) 指的是当前玩家从该状态出发所能获得的最优结果。

终止状态 (Terminal State)：游戏结束时的状态。其值是已知的，由游戏规则确定（例如，获胜得+10分，失败得-10分）。
非终止状态 (Non-Terminal State)：游戏过程中的状态。其值通过其后继状态的值递归定义。

Minimax通过对博弈树进行后序遍历，从叶节点（终止状态）开始，自底向上计算每个节点的值。

$b.$ 递归定义

我们将状态 $s$ 的值记为 $V(s)$ ，其递归定义如下：

MAX 玩家（我方）：轮到我方行动时，我们会选择能够导向最大子节点值的行动： $V(s) = \max_{s' \in \text{successors}(s)} V(s')$
MIN 玩家（对手）：轮到对手行动时，它会选择能够导向最小子节点值的行动： $V(s) = \min_{s' \in \text{successors}(s)} V(s')$
终止状态： $V(s) = \text{known value}$

$c.$ 代码实现

我们递归探索博弈树，为每个状态计算其Minimax值。根节点最终会选择那个通往值最大的子节点的行动。

def minimax_value(state):
    """
    Returns the minimax value of a state.
    """
    if state.is_terminal():
        return state.get_utility()

    if state.get_agent_to_move() == "MAX":
        # MAX player wants to maximize the value
        return max(minimax_value(successor) for successor in state.get_successors())
    else: # MIN player
        # MIN player wants to minimize the value
        return min(minimax_value(successor) for successor in state.get_successors())

def get_minimax_action(state):
    """
    Returns the optimal action for the current player on the state.
    """
    best_action = None
    best_value = -float('inf') # For MAX player

    for action in state.get_legal_actions():
        successor = state.generate_successor(action)
        value = minimax_value(successor)

        if value > best_value:
            best_value = value
            best_action = action

    return best_action

2. Alpha-Beta 剪枝

Minimax算法虽然最优，但其时间复杂度为 $O(b^m)$ （ $b$ 是分支因子， $m$ 是最大深度），对于复杂游戏来说计算量过大。Alpha-Beta剪枝是对Minimax的优化。

剪枝的核心思想是：在搜索过程中，如果一个节点的分支再怎么搜索，其最终结果都不会比当前已找到的最佳选择更好，那么这个节点和它的所有后续分支都可以被剪掉，无需再进行探索。

注意：Alpha-Beta剪枝只能用于零和博弈中！因为非零和博弈可能存在对双方都有利的选项。

$a.$ Alpha 和 Beta 值

Alpha-Beta剪枝通过维护两个值来实现剪枝：

Alpha (α)：MAX玩家在当前路径上已经找到的最高分。初始值为 $-\infty$ 。
Beta (β)：MIN玩家在当前路径上已经找到的最低分。初始值为 $+\infty$ 。

$b.$ 剪枝规则

MAX节点剪枝：在评估一个MAX节点的子节点时，如果某个子节点的值 $v$ 大于或等于 $\beta$ ，则停止评估该MAX节点的其他子节点。
MIN节点剪枝：在评估一个MIN节点的子节点时，如果某个子节点的值 $v$ 小于或等于 $\alpha$ ，则停止评估该MIN节点的其他子节点。

这种剪枝的原理如下（以MIN节点为例）：

当前情况：我们正在一个 MIN 节点（对手的回合），它的父节点是一个 MAX 节点（我方的回合）。
剪枝过程：
1. MAX玩家（父节点）通过之前的搜索，已经有了一个保底分数 $\alpha$ 。
2. 现在轮到MIN玩家（当前节点）行动，它会尝试自己的每一个走法（即遍历它的子节点），试图找到一个能让MAX玩家得分尽可能低的方案。
3. 假设MIN玩家在评估它的一个子节点时，发现这个子节点的值是 v，那么：
  - 因为MIN玩家的目标是最小化MAX的得分，所以这个MIN节点的最终得分最多也只会是 $v$ （可能还会找到更低的值）。
  - 而MAX玩家（父节点）已经有一个保底分 $\alpha$ 了，并且 $v \leq \alpha$ 。
  - 这意味着，MAX玩家绝不会选择通往当前这个MIN节点的路径，因为它有更好的选择。
  - 既然这条路肯定不会走，那么再花时间去评估这个MIN节点的其他子节点（看看能不能找到比 $v$ 更低的分数）就完全是浪费时间了。直接剪掉这个MIN节点余下的所有未评估分支。

通过这种方式，Alpha-Beta剪枝可以将最优情况下的时间复杂度降低到 $O(b^{m/2})$ ，相当于将可搜索的深度加倍。

$c.$ 一个例子

以下面这道题为例：

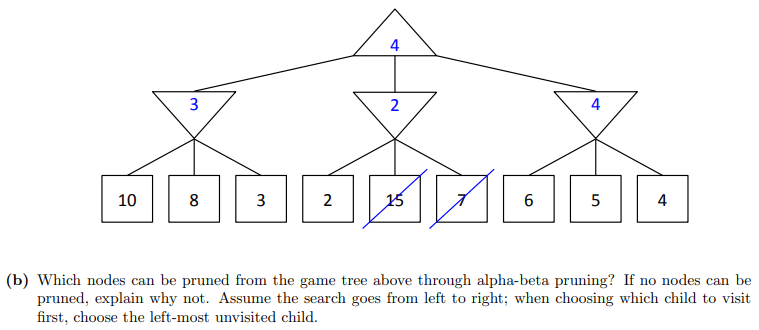
alt text

初始状态:
- 在根节点（顶部的MAX节点），我们初始化两个值：
  - $\alpha = -\infty$
  - $\beta = \infty$

第一步：搜索最左边的分支：

我们进入第一个MIN节点（向下的三角形）。它继承了父节点的 $\alpha$ 和 $\beta$ 值 ( $\alpha = -\infty, \beta = +\infty$ )。
该MIN节点开始考察它的子节点（叶子节点）：
- 遇到第一个子节点 10。对于MIN节点来说，它会更新 $beta$ 值。 $beta = \min(+∞, 10) = 10$ 。
- 遇到第二个子节点 8。 $\beta = \min(10, 8) = 8$ 。
- 遇到第三个子节点 3。 $\beta = \min(8, 3) = 3$ 。
这个MIN节点考察完了所有子节点，它的值确定为3。
将值3返回给根节点（MAX节点）。因为根节点是MAX节点，它会更新自己的 $alpha$ 值。 $\alpha = \max(-∞, 3) = 3$ 。

到目前为止，根节点知道它至少可以拿到3分。

第二步：搜索中间的分支：

我们进入第二个MIN节点。它继承父节点（根节点）当前的 $alpha$ 和 $beta$ 值 ( $\alpha = 3, \beta = +∞$ )。
该MIN节点开始考察它的子节点：
- 遇到第一个子节点 2。对于MIN节点，它会更新自己的 $beta$ 值。 $beta = \min(+∞, 2) = 2$ 。
剪枝判断：此时，在这个MIN节点上，我们发现它的值 $\leq \alpha$ $\leq α$ 。
- 这意味着什么？这意味着，对于这个MIN节点，它能得到的最好结果（最小值）最多也就是2。而根节点的MAX玩家在第一步中已经找到了一个可以确保拿到3分的路径。因此，MAX玩家绝不会选择这条通往中间MIN节点的路径。
- 既然MAX玩家不会走这条路，那么这个MIN节点剩下的子节点（15 和 7）就完全没有必要再考察了。
- 我们执行剪枝操作，将值为15和7的这两个节点剪掉。

第三步：搜索最右边的分支

我们进入第三个MIN节点。它继承根节点当前的 $alpha$ 和 $beta$ 值 ( $\alpha = 3, \beta = +∞$ )。
该MIN节点开始考察它的子节点：
- 遇到第一个子节点 6。更新 $\beta = \min(+∞, 6) = 6$ 。此时 $6 \gt \alpha(3)$ ，不剪枝。
- 遇到第二个子节点 5。更新 $\beta = min(6, 5) = 5$ 。此时 $5 > \alpha(3)$ ，不剪枝。
- 遇到第三个子节点 4。更新 $\beta = min(5, 4) = 4$ 。此时 $4 > \alpha(3)$ ，不剪枝。
这个MIN节点考察完了所有子节点，它的值确定为4。
将值4返回给根节点。根节点更新 $\alpha = \max(3, 4) = 4$ 。

通过alpha-beta剪枝，最终可以被剪掉的节点是值为 15 和 7 的叶子节点。

$d.$ 代码实现

def alpha_beta_search(state):
    """
    Performs alpha-beta search to find the best action.
    """

    def max_value(state, alpha, beta):
        if state.is_terminal():
            return state.get_utility()
        v = -float('inf')
        for action in state.get_legal_actions():
            successor = state.generate_successor(action)
            v = max(v, min_value(successor, alpha, beta))
            if v >= beta:
                return v # Prune
            alpha = max(alpha, v)
        return v

    def min_value(state, alpha, beta):
        if state.is_terminal():
            return state.get_utility()
        v = float('inf')
        for action in state.get_legal_actions():
            successor = state.generate_successor(action)
            v = min(v, max_value(successor, alpha, beta))
            if v <= alpha:
                return v # Prune
            beta = min(beta, v)
        return v

    # Find the best action from the root
    best_action = None
    alpha = -float('inf')
    beta = float('inf')

    # The root is a MAX node
    best_score = -float('inf')
    for action in state.get_legal_actions():
        successor = state.generate_successor(action)
        score = min_value(successor, alpha, beta)
        if score > best_score:
            best_score = score
            best_action = action
        alpha = max(alpha, best_score)

    return best_action

3. 评估函数 (Evaluation Functions)

对于象棋、围棋等复杂游戏，搜索到终止状态是不现实的。因此，我们采用深度受限（Depth-Limited）的搜索，并在达到预设深度时，使用评估函数来估算当前非终止状态的“优劣”。

评估函数接收一个状态 $s$ ，并输出一个分数值，该分数值是对该状态真实Minimax值的估计。一个好的评估函数应该为“更好”的状态赋予更高的分数。

使用评估函数意味着放弃了Minimax的最优性保证，但换来了在有限时间内的可行决策。通常，搜索深度越深，评估函数越精确，智能体的表现就越接近最优。

$a.$ 线性特征组合

设计评估函数最常见的方法是特征的线性组合：

Eval(s) = w_1 f_1(s) + w_2 f_2(s) + \dots + w_n f_n(s)

$f_i(s)$ ：从状态 $s$ 中提取的第 $i$ 个特征，是一个可量化的数值。例如，在跳棋中，特征可以是“我方棋子数量”等。
$w_i$ ：与特征 $f_i$ 对应的权重，反映了该特征的重要性。权重可正可负。

Minimax 算法

1. Minimax 核心思想

a.a.a. 状态值

b.b.b. 递归定义

c.c.c. 代码实现

2. Alpha-Beta 剪枝

a.a.a. Alpha 和 Beta 值

b.b.b. 剪枝规则

c.c.c. 一个例子

d.d.d. 代码实现