神经网络补充

1. 神经网络架构

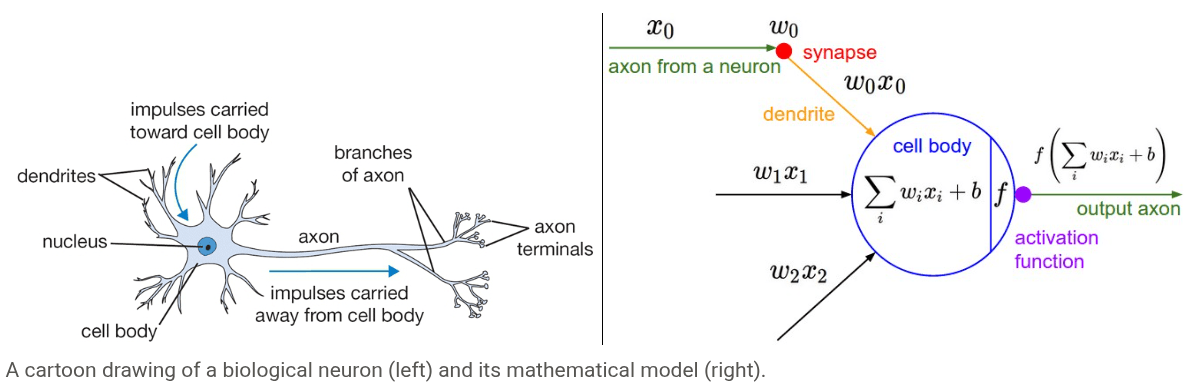
生物神经元具有如下的结构：

树突 (Dendrites)：像天线一样，负责从其他神经元那里接收输入信号。
轴突 (Axon)：是一条单一的输出线，负责将处理后的信号传递出去。
突触 (Synapses)：是轴突的末梢和其他神经元树突的连接点，是信号传递的关键节点。

简单来说，一个生物神经元就是一个信息处理器：从树突接收信息，在细胞体内处理，然后通过轴突发送结果。

我们可以将生物神经元模型抽象成一个数学模型：

输入信号 (Signals)：其他神经元传来的信号，在模型中被表示为数值，如 $x_0$ 。
突触强度 (Synaptic Strength)：在生物上，一个神经元对另一个的影响力有强有弱。在模型中，这被抽象为权重 (weights)，如 $w_0$ $w_{0}$ 。
- 权重 $w$ 是整个神经网络学习的关键。模型通过调整权重来“学习”知识。
- 权重的方向：
  - 正权重 (Excitory)：代表“兴奋性”连接，即一个神经元的激发会促进下一个神经元的激发。
  - 负权重 (Inhibitory)：代表“抑制性”连接，即一个神经元的激发会抑制下一个神经元的激发。
信号的交互：生物信号通过突触时，其效果受突触强度的影响。在模型中，这个过程被简化为一次简单的乘法运算 $w_0 * x_0$ 。

在生物神经元中，所有从树突接收到的信号汇集到细胞体并累加。如果这个总和的强度超过了某个阈值，神经元就会被激发，沿着轴突发送一个脉冲信号。这是一个“有或无”的二元事件。

而对应的数学模型中，我们简化掉每一次脉冲的精确时间点，而是关心它在一段时间内的激发频率。强的总输入信号对应高的激发频率，弱的信号对应低的激发频率。信息通过频率来编码。

为了模拟激发频率，我们引入激活函数 $f$ 。激活函数接收上一步计算出的加权总和 $w_0x_0+w_1x_1+\cdots$ ，并输出一个值，这个值就代表了该神经元的激发频率。

因此整理而成的数学模型中的信息处理流程如下：

将所有输入信号 $x$ 与其对应的连接权重 $w$ 相乘，得到加权后的输入。
用激活函数来求和计算最终的激发频率。

alt text

2. 作为分类器的单独神经元

神经元的数学模型的信息处理流程类似线性分类器：模型在信号处理过程中的 $wx+b$ 正是线性分类器的决策函数形式。它在输入空间中定义了一个线性边界。

但是神经元本身只会进行一次前向计算，它不知道自己的输出是对是错。要让它“学习”并成为一个分类器，我们必须给它一个目标，这个目标是通过损失函数来定义的。损失函数用来衡量神经元预测结果的“糟糕程度”。

$a.$ 二元 Softmax 分类器（逻辑回归）

在逻辑回归分类器中，我们将神经元的输出 $a=\sigma(wx+b)$ 解释为输入样本 $x$ 属于类别1的概率，即 $P(y=1 \mid x; w)$ 。由于是二元分类，另一类别的概率为 $P(y=0 \mid x;w) = 1 - P(y=1 \mid x; w)$ 。

对于这个分类器，我们使用交叉熵损失进行训练，通过梯度下降等优化算法来最小化交叉熵损失函数：

L = -\sum _i y_i \log p_i

由于 Sigmoid 函数的特性，当 $wx + b \gt 0$ 时，输出 $\sigma(...) \gt 0.5$ ；当 $wx + b \lt 0$ 时，输出 $\sigma(...) \lt 0.5$ 。因此，训练完成后，我们用0.5作为阈值来做预测：输出大于0.5则判为类别1，否则判为类别0。

$b.$ 二元 SVM（支持向量机）分类器

在二元SVM分类器中，我们不再将输出 $z = wx + b$ 看作概率，而是看作一个决策分数。

我们不再使用交叉熵损失，而是给神经元的输出附加一个最大间隔合页损失。它的目标比“做对分类”更苛刻。它不仅要求分类正确，还要求正确的一方要与决策边界有足够的间隔。它会惩罚那些离边界太近的“不安全”的点，从而迫使模型学习到一个泛化能力更强的、位于两个类别中间的决策边界：

L(y, f(x)) = max(0, 1 - yf(x))

$c.$ 正则化——训练遗忘

在训练分类器时，我们通常会在损失函数上增加一个正则化项（如 $λ ||w||^2$ ），目的是惩罚过大的权重，防止模型过拟合。这个操作会在每次参数更新时，都将权重 $w$ 向零拉近一点。

如果我们将权重 $w$ 视作生物神经元之间的 “突触强度”或“记忆”。那么，正则化项不断将权重拉向零的效果，就可以被解释为一种 “渐进遗忘 (gradual forgetting)” 的过程。这意味着，如果一个连接没有在数据中被反复、强烈地激活，它就会随着时间的推移慢慢衰减。这与生物大脑中记忆的工作方式有相似之处。

3.神经网络架构

$a.$ 神经网络的层级架构

神经元组成无环图：
- 神经网络被看作是由神经元组成的图。一些神经元的输出是另一些神经元的输入。
- 这个图必须是无环的，否则在前向计算时会陷入无限循环。
全连接层：
- 这是最常见的层类型。它的特点是：相邻两层之间的所有神经元都两两完全连接。
- 但是，同一层内的神经元之间没有任何连接。

与网络中的隐藏层不同，输出层的神经元通常没有激活函数。输出层的任务是产出最终结果，不需要被压缩到特定范围。

$b.$ 前向计算

在将神经网络组织成层之后，我们就可以用非常高效的矩阵和向量运算来完成整个网络的计算：

我们将输入视为向量 $x$ 。
将每一层的连接权重组织成矩阵 $W$ 。
每一层的偏置构成向量 $b$ 。
每一层的计算包括矩阵乘法、偏置相加和激活函数计算：

f = lambda x: 1.0/(1.0 + np.exp(-x)) # Define activation function (Sigmoid)
x = np.random.randn(3, 1)            # [3x1]

# First Hidden Layer Calculation
h1 = f(np.dot(W1, x) + b1)           # [4x1]

神经网络补充

1. 神经网络架构

2. 作为分类器的单独神经元

a.a.a. 二元 Softmax 分类器（逻辑回归）

b.b.b. 二元 SVM（支持向量机）分类器

c.c.c. 正则化——训练遗忘