深度学习自然语言处理

• 87 min read • 17341 words
Tags: Deep Learning NLP
Categories: NLP

深度学习自然语言处理

1. 引入

在之前的讨论中，我们已经明确了非线性分类器的必要性，因为大多数数据并不是线性可分的，因此使用线性分类器的分类性能会受到限制。

神经网络是一类具有非线性决策边界的分类器。

2. 神经元

a.a. 相关概念

神经元是一个通用的计算单元，它接受 nn 个输入并产生一个输出。

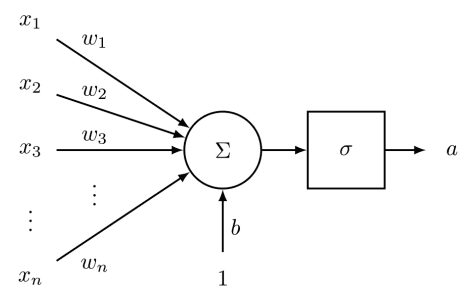
一个比较常见的神经元类型是 SigmoidSigmoid 逻辑单元，神经元关联着一个 nn 维权重向量 ww 和一个标量偏置 bb，其输出为：

a=11+exp⁡(−[wT b]⋅[x 1])a = \frac{1}{1 + \exp(-[w^T \ b] \cdot [x \ 1])}

其传递方式如下图：

alt text

b.b. 单层神经元

我们将上述概念扩展到多个神经元，考虑将输入 xx 作为输入馈送给多个这样的神经元。果我们将不同神经元的权重称为 {w(1),⋯ ,w(m)w^{(1)}, \cdots, w^{(m)}}，偏置称为 {b1,⋯ ,bmb_1, \cdots, b_m}，则相应的激活值是 {a1,⋯ ,ama_1, \cdots, a_m}：

a1=11+exp⁡(w(1)Tx+b1),...,am=11+exp⁡(w(m)Tx+bm)a_1 = \frac{1}{1 + \exp(w^{(1)T}x + b_1)} ,. . . ,a_m = \frac{1}{1 + \exp(w^{(m)T}x + b_m)}

c.c. 一些符号的定义

为了便于表达，我们定义以下的符号：

  • σ(z)=[11+exp⁡(z1)⋮11+exp⁡(zm)]\sigma(z) = \begin{bmatrix} \frac{1}{1+\exp(z_1)} \\ \vdots \\ \frac{1}{1+\exp(z_m)} \end{bmatrix}
  • b=[b1⋮bm]∈Rmb = \begin{bmatrix} b_1 \\ \vdots \\ b_m \end{bmatrix} \in \mathbb{R}^m
  • W=[−w(1)T−⋮−w(m)T−]∈Rm×nW = \begin{bmatrix} - w^{(1)T} - \\ \vdots \\ - w^{(m)T} - \end{bmatrix} \in \mathbb{R}^{m \times n}

现在我们就可以将缩放和偏置的输出写为：

z=Wx+bz = Wx + b

而 SigmoidSigmoid 函数的激活值可以写为：

[a1⋮am]=σ(z)=σ(Wx+b)\begin{bmatrix} a_1 \\ \vdots \\ a_m \end{bmatrix} = \sigma(z) = \sigma(Wx + b)

这些激活值可以作为一系列指标集合，我们可以进一步组合这些特征值来执行分类任务。

这也是为什么我们要一个中间层 aa， 而不是直接从 xx 中得到答案。我们想让模型学习到更复杂、更强大的 “组合特征”或“交互关系”，而不仅仅是单个输入特征。

d.d. 不同层的交互流程

  1. z=Wx+bz = Wx + b：使用神经元来处理输入层传入的 xx，给 xx 中对应的数据分配对应的权重并加上自己的偏移量 bb。
  2. a=σ(z)a = \sigma(z)：将 zz 通过拟合sigmoidsigmoid 压缩到 [0,1][0, 1] 间，得到激活值。
  3. s=UTas = U^Ta：将所有神经元的激活值进行加权求和，得到最终的单一决策分数 ss。

3. 反向传播

a.a. 最大间隔目标函数

像大多数机器学习模型一样，神经网络也需要一个优化目标函数。

假设一个问题的正确结果为 resres， 我们将神经元计算的 resres 为真的分数记为 ss，将计算的 resres 为假的分数记为 scs_c，其中：

sc=UTf(Wxc+b),s=UTf(Wx+b)s_c = U^Tf(Wx_c + b), s = U^Tf(Wx + b)

我们的目标函数就变成 min⁡(sc−s)\min(s_c - s)（我们更习惯求最小值而不是求最大值）。

进一步地，我们只关注 ss 是否高于 scs_c，因此目标函数变为：

min⁡J=max⁡(sc−s,0)\min J=\max(s_c-s, 0)

然而，如果 scs_c 和 ss 过于接近，那么神经元很可能会预测出错误的结果。因此，我们引入安全边界，让 ss 的值至少比 scs_c 高出 Δ\Delta，我们的目标函数变为：

min⁡J=max⁡(sc−s+Δ,0)\min J=\max(s_c-s+\Delta, 0)

b.b. 使用反向传播进行计算

我们讨论当 JJ 为正时，我们如何训练模型中的不同参数。我们通常使用梯度下降的方法来更新参数。我们需要知道参数的梯度信息：

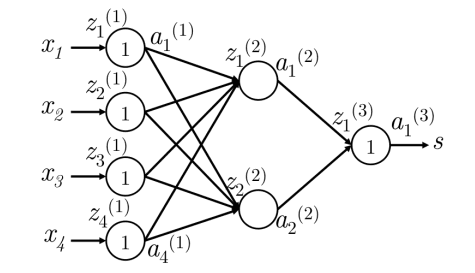
θ(t+1)=θ(t)−α∇θ(t)J\theta^{(t+1)} = \theta^{(t)} - \alpha \nabla_{\theta^{(t)}} J

我们可以通过链式法则来计算任意参数的损失梯度。我们以下面的神经网络为例：

alt text

i.i. 符号声明
  • xix_i：神经网络的输入。
  • ss： 神经网络的输出。
  • 每一层（包括输入层和输出层）都有接收输入并产生输出的神经元。第 kk 层的第 jj 个神经元接收标量输入 zj(k)z_j^{(k)} 并产生标量激活输出 aj(k)a_j^{(k)}。
  • 我们将在 zj(k)z_j^{(k)} 处计算的反向传播误差称为 δj(k)\delta_j^{(k)}。
  • 第 1 层指的是输入层，而不是第一个隐藏层。对于输入层，xj=zj(1)=aj(1)x_j = z_j^{(1)} = a_j^{(1)}。
  • Wij(k)W^{(k)}_{ij} ：将第 kk 层的输出映射到第 (k+1)(k+1) 层输入的转换矩阵。连接的方向为 j→ij\rightarrow i。
  • 为保持定义与符号的统一，我们让：W(1)=WW^{(1)} = W 且 W(2)=UW^{(2)} = U。
ii.ii. 从数学角度的推导

首先应该明确： W14(1)W_{14}^{(1)} 只对 z1(2)z_1^{(2)} 有贡献，因此也只对 a1(2)a_1^{(2)} 有贡献。这个事实对于理解反向传播至关重要——反向传播的梯度只受它们所贡献的值的影响。

而在我们的损失函数 sc+1−ss_c + 1 - s 中，有：

∂J∂s=−∂J∂sc=−1\frac{\partial J}{\partial s} = - \frac{\partial J}{\partial s_c} = -1

则：

∂s∂Wij(1)=∂W(2)a(2)∂Wij(1)=∂Wi(2)ai(2)∂Wij(1)=Wi(2)∂ai(2)∂Wij(1)\begin{aligned} \frac{\partial s}{\partial W_{ij}^{(1)}} = \frac{\partial W^{(2)} a^{(2)}}{\partial W_{ij}^{(1)}} = \frac{\partial W_i^{(2)} a_i^{(2)}}{\partial W_{ij}^{(1)}} = W_i^{(2)} \frac{\partial a_i^{(2)}}{\partial W_{ij}^{(1)}} \\ \end{aligned} ⇒Wi(2)∂ai(2)∂Wij(1)=Wi(2)∂ai(2)∂zi(2)∂zi(2)∂Wij(1)=Wi(2)f(zi(2))∂zi(2)∂zi(2)∂zi(2)∂Wij(1)=Wi(2)f′(zi(2))∂zi(2)∂Wij(1)=Wi(2)f′(zi(2))∂∂Wij(1)(bi(1)+a1(1)Wi1(1)+a2(1)Wi2(1)+a3(1)Wi3(1)+a4(1)Wi4(1))=Wi(2)f′(zi(2))∂∂Wij(1)(bi(1)+∑kak(1)Wik(1))=Wi(2)f′(zi(2))aj(1)=δi(2)⋅aj(1)\begin{aligned} &\Rightarrow W_i^{(2)} \frac{\partial a_i^{(2)}}{\partial W_{ij}^{(1)}} = W_i^{(2)} \frac{\partial a_i^{(2)}}{\partial z_i^{(2)}} \frac{\partial z_i^{(2)}}{\partial W_{ij}^{(1)}} \\ &= W_i^{(2)} f(z_i^{(2)}) \frac{\partial z_i^{(2)}}{\partial z_i^{(2)}} \frac{\partial z_i^{(2)}}{\partial W_{ij}^{(1)}} \\ &= W_i^{(2)} f'(z_i^{(2)}) \frac{\partial z_i^{(2)}}{\partial W_{ij}^{(1)}} \\ &= W_i^{(2)} f'(z_i^{(2)}) \frac{\partial}{\partial W_{ij}^{(1)}} \left( b_i^{(1)} + a_1^{(1)} W_{i1}^{(1)} + a_2^{(1)} W_{i2}^{(1)} + a_3^{(1)} W_{i3}^{(1)} + a_4^{(1)} W_{i4}^{(1)} \right) \\ &= W_i^{(2)} f'(z_i^{(2)}) \frac{\partial}{\partial W_{ij}^{(1)}} \left( b_i^{(1)} + \sum_k a_k^{(1)} W_{ik}^{(1)} \right) \\ &= W_i^{(2)} f'(z_i^{(2)}) a_j^{(1)} \\ &= \delta_i^{(2)} \cdot a_j^{(1)} \end{aligned}

梯度简化为 δi(2)⋅aj(1)\delta_i^{(2)} \cdot a_j^{(1)} 的乘积，其中 δi(2)\delta_i^{(2)} 本质上是从第 2 层第 i 个神经元向后传播的误差。aj(1)a_j^{(1)} 是在按 WijW_{ij} 缩放后馈送到第 2 层第 i 个神经元的输入。

可以将这个公式理解为：一个权重的总责任=下游节点错误×自己发送的信号强度\text{一个权重的总责任}= \text{下游节点错误} \times \text{自己发送的信号强度}

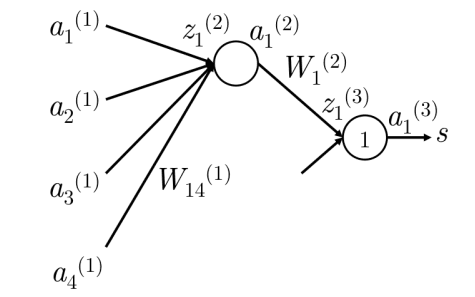
iii.iii. 从传播流程角度的推导

我们以下面这个网络为例：

alt text

  1. 我们从一个从 a1(3)a_1^{(3)} 向后传播的误差信号 1 开始。
  2. 我们将这个误差乘以将 z1(3)z_1^{(3)} 映射到 a1(3)a_1^{(3)} 的神经元的局部梯度。在这种情况下恰好是 1，因此误差仍然是 1。这现在被称为 δ1(3)=1\delta_1^{(3)} = 1。
  3. 此时，误差信号 1 已经到达 z1(3)z_1^{(3)}。我们现在需要分配误差信号，以便“公平份额”的误差到达 a1(2)a_1^{(2)}。这个量是（在 z1(3)z_1^{(3)} 处的误差信号 = δ1(3)\delta_1^{(3)}）×W1(2)=W1(2)\times W_1^{(2)} = W_1^{(2)}。因此，在 a1(2)a_1^{(2)} 处的误差是 W1(2)W_1^{(2)}。
  4. 正如我们在步骤 2 中所做的，我们需要将误差移动过将 z1(2)z_1^{(2)} 映射到 a1(2)a_1^{(2)} 的神经元。我们通过将 a1(2)a_1^{(2)} 处的误差信号乘以神经元的局部梯度来做到这一点，这个梯度恰好是 f′(z1(2))f'(z_1^{(2)})。
  5. 因此，z1(2)z_1^{(2)} 处的误差信号是 f′(z1(2))W1(2)f'(z_1^{(2)}) W_1^{(2)}。这被称为 δ1(2)\delta_1^{(2)}。
  6. 最后，我们需要将误差的“公平份额”分配给 W14(1)W_{14}^{(1)}，只需将其乘以它负责转发的输入，这个输入恰好是 a4(1)a_4^{(1)}。

因此，损失相对于 W14(1)W_{14}^{(1)} 的梯度计算为 a4(1)f′(z1(2))W1(2)a_4^{(1)} f'(z_1^{(2)}) W_1^{(2)}。

c.c. 偏置项更新

偏置项b1(1)b_1^{(1)}在数学上等同于对神经元输入（z1(2)z_1^{(2)}）有贡献的其他权重，只要其前向传播的输入为 1。因此，第 kk 层第 ii 个神经元的偏置梯度就是 δi(k)\delta_i^{(k)}。例如，如果我们更新的是 b1(1)b_1^{(1)} 而不是上面的 W14(1)W_{14}^{(1)}，梯度就将是 f′(z1(2))W1(2)f'(z_1^{(2)})W_1^{(2)}。

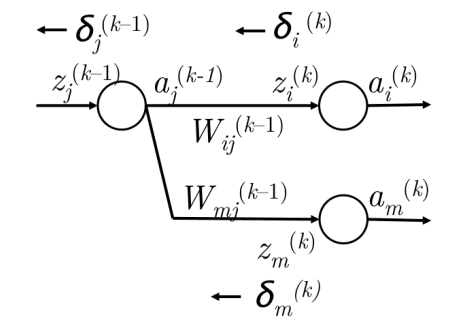
d.d. 反向传播的广义步骤

将 δ(k)\delta^{(k)} 传播到 δ(k−1)\delta^{(k-1)} 的广义步骤如下：

alt text

  1. 我们通过将 δi(k)\delta_i^{(k)} 乘以路径权重 Wij(k−1)W_{ij}^{(k-1)}，将此误差反向传播到 aj(k−1)a_j^{(k-1)}。
  2. 在 aj(k−1)a_j^{(k-1)} 处接收到的误差是 δi(k)Wij(k−1)\delta_i^{(k)} W_{ij}^{(k-1)}。
  3. 然而，aj(k−1)a_j^{(k-1)} 可能已被前向传播到下一层的多个节点。它也应该使用完全相同的机制，承担从第 kk 层节点 mm 反向传播而来的误差的责任。因此，在 aj(k−1)a_j^{(k-1)} 处接收到的误差是 δi(k)Wij(k−1)+δm(k)Wmj(k−1)\delta_i^{(k)} W_{ij}^{(k-1)} + \delta_m^{(k)} W_{mj}^{(k-1)}。

实际上，我们可以将其推广为 ∑iδi(k)Wij(k−1)\sum_i \delta_i^{(k)} W_{ij}^{(k-1)}。

  1. 现在我们得到了在 aj(k−1)a_j^{(k-1)} 处的正确误差，我们通过乘以局部梯度 f′(zj(k−1))f'(z_j^{(k-1)}) 将其传递过第 k-1 层的神经元 j。 因此，到达 zj(k−1)z_j^{(k-1)} 的误差，称为 δj(k−1)\delta_j^{(k-1)}，是 f′(zj(k−1))∑iδi(k)Wij(k−1)f'(z_j^{(k-1)}) \sum_i \delta_i^{(k)} W_{ij}^{(k-1)}

e.e. 反向传播的向量化

到目前为止，我们讨论了如何计算模型中给定参数的梯度。在这里，我们将推广上述方法，以便我们可以一次性更新权重矩阵和偏置向量。

对于给定的参数 Wij(k)W_{ij}^{(k)}，我们确定了误差梯度就是 δi(k+1)⋅aj(k)\delta_i^{(k+1)} \cdot a_j^{(k)}。因此，我们可以确定整个矩阵 W(k)W^{(k)} 的误差梯度是：

∇W(k)=[δ1(k+1)a1(k)δ1(k+1)a2(k)⋯δ2(k+1)a1(k)δ2(k+1)a2(k)⋯⋮⋮⋱]=δ(k+1)a(k)T\nabla_{W^{(k)}} = \begin{bmatrix} \delta_1^{(k+1)} a_1^{(k)} & \delta_1^{(k+1)} a_2^{(k)} & \cdots \\ \delta_2^{(k+1)} a_1^{(k)} & \delta_2^{(k+1)} a_2^{(k)} & \cdots \\ \vdots & \vdots & \ddots \end{bmatrix} = \delta^{(k+1)} a^{(k)T}

因此，我们可以使用传播到矩阵的误差向量和由该矩阵前向传播的激活值的外积来编写整个矩阵梯度。我们可以将广义步骤中得到的公式推广到矩阵上：

δ(k)=f′(z(k))∘(W(k)Tδ(k+1))\delta^{(k)} = f'(z^{(k)}) \circ (W^{(k)T} \delta^{(k+1)})

我们应该减少反向传播中的冗余计算——例如，注意到 δ(k)\delta^{(k)} 直接依赖于 δ(k+1)\delta^{(k+1)}。因此，我们应该确保当我们使用 δ(k+1)\delta^{(k+1)} 更新 W(k)W^{(k)} 时，我们保存 δ(k+1)\delta^{(k+1)} 以便稍后推导出 δ(k)\delta^{(k)}——然后我们对 (k−1)...(1)(k-1)...(1) 重复这个过程。这样的递归过程使得反向传播成为一个计算上可行的过程。

4. 正则化

a.a. 相关概念

与许多机器学习模型一样，神经网络非常容易过拟合，即模型能够在训练数据集上获得近乎完美的性能，但丧失了对未见数据的泛化能力。解决过拟合的一种常用技术是引入 L2L2 正则化惩罚项。其思想是，我们只需在损失函数 JJ 上附加一个额外的项，这样总成本就计算为：

JR=J+λ∑i=1L∣∣W(i)∣∣F2J_R = J + \lambda \sum_{i=1}^{L} ||W^{(i)}||_F^2

矩阵 U 的弗罗贝尼乌斯范数定义如下： ∣∣U∣∣F=∑i∑jUij2||U||F = \sqrt{\sum_i \sum_j U{ij}^2}

在上述公式中，∣∣W(i)∣∣F2||W^{(i)}||_F^2 是矩阵 W(i)W^{(i)}（网络中第 i 个权重矩阵）的弗罗贝尼乌斯范数的平方，而 λ\lambda 是一个超参数，用于控制正则化项相对于原始成本函数的权重。由于我们试图最小化 JRJ_R，正则化的本质是在优化原始成本函数的同时，对过大的权重进行惩罚。

由于弗罗贝尼乌斯范数的二次性质，L2L2 正则化有效地降低了模型的灵活性，从而减少了过拟合现象。施加这样的约束也可以解释为一种先验的贝叶斯信念，即最优权重接近于零——具体多接近取决于 λ\lambda 的值。选择正确的 λ\lambda 值至关重要，必须通过超参数调整来选择。λ\lambda 值过高会导致大多数权重被设置得太接近 0，模型无法从训练数据中学到任何有意义的东西，通常在训练集、验证集和测试集上都表现不佳。值太低，我们又会再次陷入过拟合的境地。

必须注意的是，偏置项不被正则化，也不对上述成本项做出贡献。因为模型的主要“复杂度”和“容量”都体现在权重上。

我们先验地认为，一个**更简单的模型（权重值更接近于0的模型）**是更好的模型。

b.b. Dropout 方法

Dropout 是一种强大的正则化技术，其思想简单而有效：在训练期间，我们在每次前向/后向传播过程中，以一定的概率（1−p1-p）随机“丢弃”一部分神经元（或者等价地说，我们以概率 pp 保留每个神经元）。然后在测试期间，我们使用完整的网络来计算我们的预测。结果是，网络通常能从数据中学习到更有意义的信息，更不容易过拟合，并且通常在当前任务上获得更高的整体性能。这项技术之所以如此有效，一个直观的原因是，dropout 本质上是在同时训练指数级数量的较小网络，并对它们的预测进行平均。

在实践中，我们引入 Dropout 的方式是，我们取每层神经元的输出 hh，并以概率 pp 保留每个神经元，否则将其设置为0。然后，在反向传播期间，我们只让梯度通过那些在前向传播中被保留下来的神经元。最后，在测试期间，我们使用网络中的所有神经元计算前向传播。

然而，一个关键的细节是，为了让 dropout 有效地工作，测试期间神经元的期望输出应与训练期间大致相同——否则输出的量级可能会有根本的不同，网络的行为就不再是良定义的。因此，我们通常必须在测试期间将每个神经元的输出乘 pp，使训练和测试期间的期望输出相等。

5. 神经元单元

我们列举一些常见的激活函数：

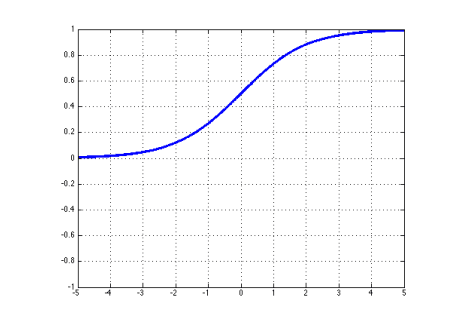
  • Sigmoid：这是我们在讨论中使用的选择；激活函数 σ\sigma 由下式给出：
σ(z)=11+exp⁡(−z)\sigma(z) = \frac{1}{1 + \exp(-z)}

其梯度为：

σ′(z)=−exp⁡(−z)1+exp⁡(−z)=σ(z)(1−σ(z))\sigma'(z) = -\frac{\exp(-z)}{1 + \exp(-z)} = \sigma(z)(1 - \sigma(z))

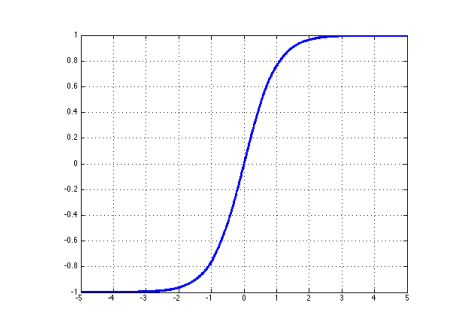
alt text

  • Tanh：tanh 函数是 sigmoid 函数的一种替代方案，在实践中通常发现它收敛得更快。tanh 和 sigmoid 的主要区别在于 tanh 的输出范围是 -1 到 1，而 sigmoid 的范围是 0 到 1：
tanh⁡(z)=exp⁡(z)−exp⁡(−z)exp⁡(z)+exp⁡(−z)=2σ(2z)−1\tanh(z) = \frac{\exp(z) - \exp(-z)}{\exp(z) + \exp(-z)} = 2\sigma(2z) - 1

其梯度为：

tanh⁡′(z)=1−(exp⁡(z)−exp⁡(−z)exp⁡(z)+exp⁡(−z))2=1−tanh⁡2(z)\tanh'(z) = 1 - \left( \frac{\exp(z) - \exp(-z)}{\exp(z) + \exp(-z)} \right)^2 = 1 - \tanh^2(z)

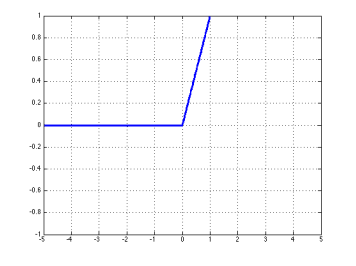
alt text

  • ReLU：ReLU（修正线性单元）函数是一种流行的激活函数选择，因为它即使在 zz 值较大时也不会饱和：
rect(z)=max⁡(z,0)\text{rect}(z) = \max(z, 0)

其梯度为：

rect′(z)={1:z>0 0:otherwise\text{rect}'(z) = \begin{cases} 1 & : z > 0 \ 0 & : \text{otherwise} \end{cases}

alt text

6. 数据预处理

与一般的机器学习模型一样，要确保模型在特定任务上获得合理的性能，一个关键步骤是对数据进行基本的预处理。下面是一些常用的技术。

a. 均值减法

给定一组输入数据 XX，通常的做法是通过从 XX 中减去其平均特征向量来对数据进行零中心化。重要的一点是，在实践中，均值仅在训练集上计算，然后将这个均值从训练集、验证集和测试集中减去。

b. 归一化

另一种常用的技术（尽管可能不如均值减法常用）是缩放每个输入特征维度，使其具有相似的量级范围。这很有用，因为输入特征通常以不同的“单位”来衡量，但我们通常希望在初始阶段将所有特征视为同等重要。我们实现这一点的方法是，简单地将特征除以它们在训练集上计算出的各自的标准差。

c. 白化

白化不像均值减法+归一化那样常用，它本质上是将数据转换为具有单位协方差矩阵——也就是说，特征变得不相关并且方差为 1。这通常通过首先对数据进行均值减法来完成，得到 X′X'。然后我们可以对 X′X' 进行奇异值分解（SVD）得到矩阵 U,S,VU, S, V。接着我们计算 UTX′U^T X' 将 X′X' 投影到由 UU 的列定义的基上。最后，我们将结果的每个维度除以 SS 中对应的奇异值来适当地缩放我们的数据（如果某个奇异值为零，我们可以用一个很小的数来代替除法）。