循环神经网络

1. 语言模型

$a.$ 介绍

语言模型的主要任务是计算一个词语序列出现的概率有多大。一个由 $m$ 个词组成的序列 $\lbrace w_1, ..., w_m \rbrace$，它出现的概率被记为 $P(w_1, ..., w_m)$。

要直接计算整个句子的概率非常困难。我们使用条件概率公式将其分解：一个句子的概率，等于第一个词的概率，乘在第一个词出现的情况下第二个词出现的概率，再乘以在前两个词都出现的情况下第三个词出现的概率，以此类推：

在现实中，要考虑一个词前面所有的历史词语，计算量巨大且数据稀疏（很多词语组合在训练数据中根本没出现过）。因此，我们做一个简化假设（马尔科夫假设）：一个词的出现概率，并不需要依赖于前面所有的词，而*只依赖于它前面有限的 $n$ 个词**：

这个简化极大地降低了计算的复杂性，并使得语言模型在实际中变得可行。

$b.$ n-gram 语言模型

在 n-gram 语言模型中，我们采用基于统计计数的方式计算前面说的马尔科夫假设中的概率。

n-gram 中的 $n$ 是指文本中连续的 $n$ 个词语

例如，我们想用 $bigram$ 模型 ($n=2$) 计算 $P(北京 | 我爱)$ 的概率，也就是“我爱”后面出现“北京”的概率：

1. 首先，我们在巨大的语料库中统计 (我爱, 北京) 这个词组出现了多少次，例如 1000 次。
2. 然后，我们再统计 (我爱) 这个前缀出现了多少次，例如 10000 次。
3. 于是我们得到这个概率为：$\frac{1000}{10000}=0.1$

通过这种在大规模数据上进行统计的方法，模型就能学到语言的规律，比如“我爱”后面接“北京”的概率，会远高于接“香蕉”的概率。

$c.$ n-gram 模型的局限性

n-gram 模型最核心的缺陷是稀疏性问题。因为语言的组合是无限的，而我们的语料库是有限的，所以总有很多合法的词组从未在语料库中出现过。有下面两种情况：

1. 分子为 0： 如果词组 $(w_1, w_2, w_3)$ 从未在语料库中出现，它的计数就是 0，导致计算出的概率也为 0。但这并不代表这个句子不合法，可能只是我们恰好没见过。
   • 对这个问题的一个解决方案为平滑 (Smoothing)。比如拉普拉斯平滑，就是给所有 n-gram 的计数都加上一个很小的值 $δ$，确保没有任何概率是绝对的 $0$。
2. 分母为 0： 如果词对 $(w1, w2)$ 从未出现过，分母就是 0，这个概率就无法计算了。
   • 对这个问题的一个解决方案为回退 (Backoff)。如果 $trigram p(w_3|w_1, w2_)$ 因为分母为 0 无法计算，我们就退一步使用 $bigram p(w_3|w_2)$ 来近似估算。如果 $bigram$ 还不行，就再退一步用 $unigram p(w_3)$。

$n$ 越大，稀疏性问题就越严重。一个 5-gram 词组在语料库中出现的概率远低于一个 bigram 词对。因此，$n$ 通常取值很小，一般不会超过 5。

同时，n-gram 模型需要存储所有在语料库中见过的 n-gram 及其计数。这可能导致：

• 随着 $n$ 的增大，可能的 n-gram 组合数量会呈指数级爆炸式增长。
• 随着语料库的增大，见过的 n-gram 数量也会线性增长。

这两者共同导致模型需要巨大的存储空间，尤其是在 $n$ 比较大时，模型会变得非常庞大，难以部署和使用。

2. 基于窗口的神经网络语言模型

$a.$ 简介

前面提到的 n-gram 模型的稀疏性和存储问题，在机器学习领域被统称为 “维度灾难”。因为随着 $n$ 的增大，需要考虑的上下文维度（可能性）呈指数级增长，导致数据极其稀疏。

最早有效解决这个问题的是基于窗口的神经网络。它有两个主要的特点：

1. 它不再像 n-gram 那样统计词组的离散计数，而是为每个词学习一个“分布式表示”（见word-vec这篇文章），每个词被表示成一个低维、稠密的实数向量。
2. 它直接在一个神经网络中，根据这些词向量来学习词序列的概率函数。

这一模型设计有如下的

1. 解决了数据稀疏性：相似的词（如 "cat" 和 "dog"）会有相似的词向量。因此，即使模型没见过 "the dog sat on the mat"，但只要它见过 "the cat sat on themat"，它就能根据词向量的相似性，泛化出前一个句子的概率也很高。这是 n-gram 模型完全做不到的。
2. 参数共享，模型更小：模型的大小与词汇表大小和窗口大小有关，但与语料库的大小无关。它不再需要存储海量的 n-gram 计数，大大减小了模型的体积。

$b.$ 模型架构

基于窗口的语言模型的架构如下：

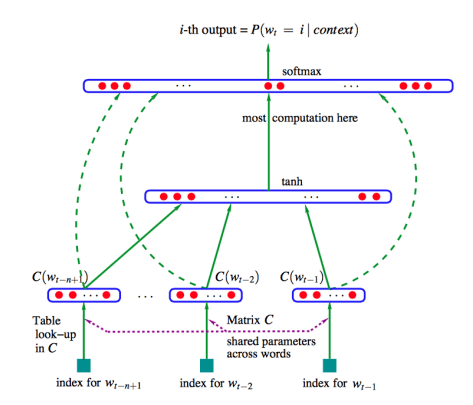
我们定义：

• $x$：模型输入，是由上下文窗口内所有单词的词向量拼接而成的一个长向量。例如，如果窗口大小是 4，每个词向量是 100 维，那么 $x$ 就是一个 400 维的向量。
• $tanh(W^{(1)}x + b^{(1)})$：标准神经网络路径。在这个路径中，输出 $x$ 首先进行线形变换映射到隐藏层,加上偏置，然后进行通过激活函数 $tanh$ 进行非线性映射。
  • 对应于从输入层到隐藏层的绿色实线箭头
• $W^{(2)}$：隐藏层输出结果经过 $W^{(2)}$ 线性变换传递到输出层
  • 对应于图1中从隐藏层到输出层的绿色实线箭头。
• $W^{(3)}x+b^{(3)}$：这是这个模型的一个独特之处。$x$ 并没有经过隐藏层，而是通过一个“直连通道”，直接进行一次线性变换，然后也被加到输出层。这可以避免隐藏层成为信息传递的唯一瓶颈，同时让梯度在反向传播时可以更直接地流向词向量层，有助于加速训练过程。
  • 对应于图1中从输入层直接连接到输出层的绿色虚线箭头。
• $softmax(...)$：标准路径和直连路径的结果相加后，再整体通过一个 softmax 函数，将一个数值向量转换成一个概率分布。输出 $\hat{y}$ 是一个维度等于整个词汇表大小的向量，其中每个元素代表对应单词是下一个词的概率，概率值最大的那个词，就是模型的最终预测。

整体流程的数学表达如下：

$c.$ 局限性

基于窗口的神经网络语言模型仍然具有如下缺陷：

1. 固定的窗口大小：模型的上下文被限制在窗口大小 $n$ 中。这意味着它仍然无法捕捉长距离依赖关系。
2. 计算效率低：在每一步预测时，输入层都是由窗口内所有词的词向量拼接而成的。权重矩阵 $W^{(1)}$ 需要与整个拼接后的长向量相乘。这意味着模型为窗口中的每个位置都学习了独立的权重。例如，应用于窗口中第一个词的权重与应用于第二个词的权重是不同的。这样会导致参数效率不高。

3. 循环神经网络

$a.$ 简介

为了解决基于窗口的神经网络，我们引入一种专门为序列数据设计的架构：循环神经网络（RNN）。

RNN 旨在处理任意长度的序列。其关键特征是拥有一个隐藏状态（hidden state），这个状态在序列的每一步都会被更新。这个隐藏状态就像是网络的“记忆”，它总结了到目前为止所有看到过的信息。

$b.$ 模型架构

RNN 语言模型按照如下的流程工作：

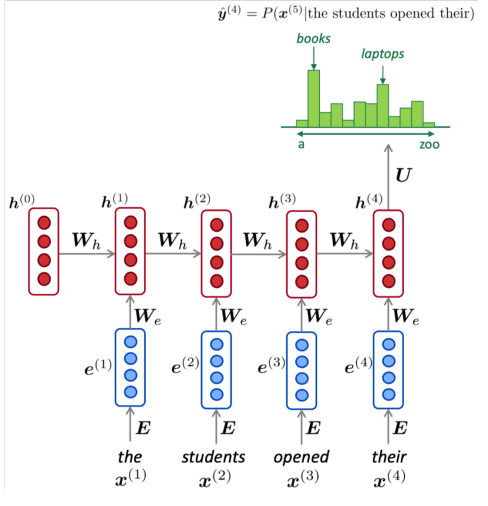
1. 初始化： 模型从一个初始的隐藏状态 $h_0$ 开始（通常是一个全零向量）。
2. 逐词处理：对于序列中的每一个词，我们进行如下操作：

输入：模型接收当前词的词向量 $x_t$。 更新隐藏状态：模型结合当前输入 $x_t$ 和前一步的隐藏状态 $h_{t-1}$，计算新的隐藏状态 $h_t$。公式为：

其中 $f$ 为激活函数 3. 进行预测：新的隐藏状态 $h_t$ 会被用于预测下一个词，这个过程通过将 $h_t$ 传入 softmax 中实现：

其中 $\hat{y_t}$ 是在整个词汇表中 $t+1$ 位置的词的概率分布。

RNN 的一个重要的特征是参数共享。在每一个时间步中，模型使用的都是同一套权重矩阵 $W_h$ 和偏置 $b_h$，网络用相同的参数来处理序列中的每一个元素。这样，无论输入序列多长，模型的参数数量是固定的。

$c.$ 局限性

RNN 语言模型具有如下的局限性：

1. 计算速度慢: RNN的计算是顺序的，必须先计算完时间步 $t-1$ 才能计算时间步 $t$。这导致它很难进行大规模的并行计算，训练和推理速度较慢。
2. 由于梯度爆炸和梯度消失，RNN很难学习到真正长距离的依赖关系。信息在传递多步后会衰减或变得过大，导致模型“遗忘”了早期的输入。

4. RNN 模型评估

$a.$ 损失函数

在单个时间步 $t$ 中，我们按照下面的方式计算损失

其中：

• $y_{t,j}$: 真实值。它是一个独热向量。在时间点 $t$，如果词汇表中的第 $j$ 个单词是正确的下一个词，那么 $y_{t,j}$ 的值就是 1，否则就是 0。
• $\hat{y}_{t,j}$: 这是模型的预测值。它表示模型预测下一个词是词汇表中第 $j$ 个词的概率。

在一个大小为 $\mid V \mid$ 的语料库中，交叉熵损失为：

$b.$ 困惑度

困惑度是衡量语言模型性能的另一个常用指，可以被理解为模型在预测下一个词时，平均下来有多少个“备选答案”。困惑度越低，说明模型对自己的预测越“确定”，性能越好。

5. 梯度爆炸与梯度下降

$a.$ 简介

在模型学习的反向传播过程中，来自遥远过去的“信息”（梯度信号）在传回来的路上逐渐减弱，甚至完全消失了。这就是梯度消失。因此，对于长句子，模型很难学习到远距离词语之间的依赖关系。

而梯度爆炸，可以通过如下的例子来理解：

我们想训练一个 RNN 来完成一个非常简单的任务：只要它看到输入的第一个词是 "go"，它就必须在后面连续输出三次 "go"。

• 输入: go
• 期望的输出: go, go, go

作为例子，我们使用一个简单的隐藏状态更新规则：

假设模型通过随机初始化，或者在训练初期，不巧将 $W$ 的值设为了 3（或其他大于 1 的数）。那么随着 $t$ 的增长，$W$ 会呈指数级增长趋势，这就是梯度爆炸：模型对最初的输入 "go" 过于兴奋了。

$b.$ 数学分析

问题的根源是链式法则中矩阵的连乘效应。

我们的目标是更新网络的权重 $W$，以减小模型的预测误差 $E$。这需要计算误差 $E$ 对权重 $W$ 的偏导数 $\frac{∂E}{∂W}$，而总的梯度等于所有时间步 $t$ 的梯度之和。在每个时间步，我们都要计算一个梯度，然后把它们加起来。：

对于单个时间步的梯度计算，我们可以使用如下的链条：

其中：

1. $\frac{∂E_t}{∂y_t}$: 最终的误差 $E_t$ 是由输出 $y_t$ 造成的。
2. $\frac{∂y_t}{∂h_t}$: 输出 $y_t$ 是由当前隐藏状态 $h_t$ 决定的。
3. $\frac{∂h_t}{∂h_k}$: 这是最关键的一环：当前隐藏状态 $h_t$ 受到了过去所有隐藏状态 $h_k$ 的影响。
4. $\frac{∂hk}{∂W}$: 过去的隐藏状态 $h_k$ 又是由权重 $W$ 决定的。

这其中的隐藏状态间的影响是导致梯度爆炸的关键所在，我们将它展开：

为了简化分析，我们不看具体的矩阵，而是看它的范数 (norm)，有：

这个不等式告诉我们，梯度在时间上传播时，其大小会被 $(β_W β_h)$ 这个因子反复缩放 $t-k$ 次。

• 如果$(β_W β_h) \lt 1$，那么就会导致梯度消失。
• 如果$(β_W β_h) \gt 1$，那么就会导致梯度爆炸。

6. 深度双向 RNN

标准的RNN在预测 $t$ 时刻的输出时，只看到了 $t$ 时刻之前的输入（历史信息）。但在很多任务中，比如理解一个句子，某个单词的真实含义不仅取决于它前面的词，也取决于它后面的词。

为了让模型能同时拥有“前瞻”和“后顾”的能力，我们提出双向 RNN 模型。而为了让模型学习更复杂、更深层次的特征，我们将其进一步扩展为深度双向RNN模型。

$a.$双向 RNN

双向RNN由下面的部分组成：

• 一个前向RNN：从左到右正常读取序列（从 $x_1$ 到 $x_T$）。
• 一个后向RNN：从右到左反向读取序列（从 $x_T$ 到 $x_1$）。

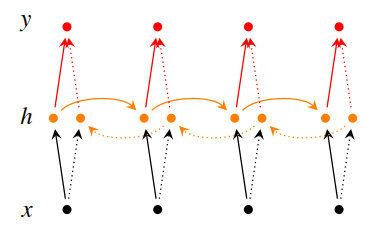
在任意一个时间点 $t$：

• 前向RNN会计算出一个前向隐藏状态 $\rightarrow h_t$。这个状态编码了从序列开始到 $t$ 时刻的历史信息。
• 后向RNN会计算出一个后向隐藏状态 $\leftarrow h_t$。这个状态编码了从序列末尾到 $t$ 时刻的未来信息。

为了得到在 $t$ 时刻最完整的表示，我们将前向和后向的隐藏状态拼接在一起，形成一个新的向量 $h_t$。这个向量 $h_t$ 同时包含了 $x_t$ 左右两侧的上下文信息。拼接后得到的 $h_t$ 会输入到 softmax 层中得到最终输出。

$b.$ 深度RNN

就像普通神经网络可以通过堆叠多个层来变得“更深”一样，RNN也可以将多个RNN层堆叠起来：第 $i$ 层的RNN的输入，是第 $i-1$ 层RNN在所有时间步上的输出序列。

$c.$ 深度双向RNN

在深度双向RNN中，网络有多个层，并且每一层都是双向的：

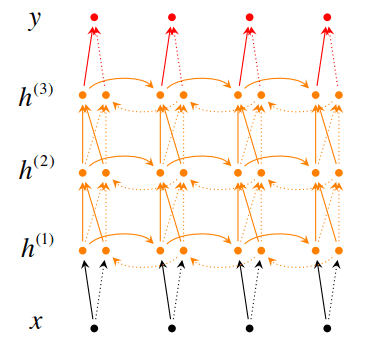
每一层的前向传播和后向传播如下：

每一层的隐藏状态更新来自：

• 第 $i-1$ 层在同一时刻 $t$ 的完整输出 $h_t^{(i-1)}$
• 第 i 层在前一时刻 $t-1$ 的前向（或后向）隐藏状态 $\rightarrow h_{t-1}^{(i)}$。

最终的模型预测如下：

7. 基于RNN的翻译模型

编码器-解码器 (Encoder-Decoder) 模型（也称为 Seq2Seq 模型）,是RNN在机器翻译中的一个应用。

$a.$ 模型架构

$i.$ 编码器

编码器是一个RNN，负责读取源语言句子（例如德语："Echt dicke Kiste"）。它在每个时间步读入一个单词，并更新其隐藏状态。

编码器的最终目标不是做预测，而是将整个句子的信息压缩进最后一个隐藏状态 $h_3$。$h_3$ 被称为上下文向量($c$)。它就像是对源语句的“思想总结”:

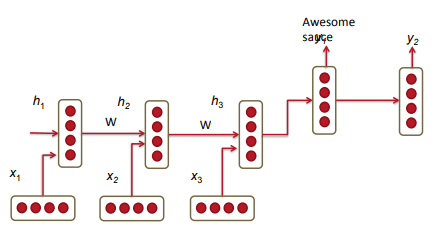
编码器的状态更新公式如下：

$ii.$ 解码器

解码器是另一个RNN，负责生成目标语言句子（例如英语："Awesome sauce"）。它将编码器产出的上下文向量 $c$ 作为其初始隐藏状态。然后它和一般的语言模型一样，一个接一个地生成目标语言的单词。最后，它根据当前隐藏状态生成一个单词的概率分布，并选择最可能的词作为输出。

解码器的状态更新公式如下：

8. 注意力机制

$a.$ 翻译模型的缺陷

基于 RNN 的翻译模型具有如下的问题：

1. 在编码器编码过程中，源句子的所有信息都会被塞进一个固定大小的向量里，很多信息可能会在压缩过程中丢失。
2. 在RNN中，信息是按顺序线性传递的。如果句子中的两个词相距很远，它们之间的信息需要经过很多个时间步才能交互。对于很长的句子，模型很难记住开头的词，因为信息在RNN中传递了太多步，导致信息衰减。
3. RNN的计算是高度串行的。要计算时间步 $t$ 的隐藏状态 $h_t$，必须先计算出 $h_{t-1}$。

$b.$ 注意力机制介绍

Attention的核心思想是：在解码器的每一步，都允许它直接“回看”并“关注”源句子的特定部分：

• 它不再强迫编码器将所有信息压缩成一个向量，而是保留编码器在每个时间步的所有隐藏状态$(h_1, h_2, ..., h_T)$。
• 解码器在生成每个词时，会根据当前需要，动态地决定给编码器的哪些隐藏状态分配更多的“注意力”。

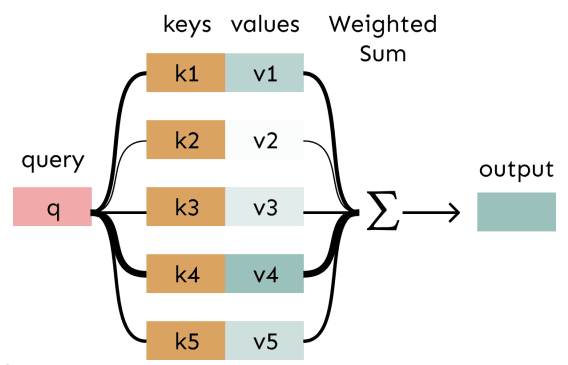
对编码器中所有的隐藏状态，Attention 使用更智能的加权平均。这个“权重”是动态计算并学习的：在Attention中，当前解码器的隐藏状态（Query）会和源句子的所有部分（也就是编码器的每个隐藏状态，Keys）进行“软匹配”，得到一个0到1之间的相似度分数（权重）。最终的结果是所有值根据这些权重进行的加权总和：

$c.$ 在 Seq2Seq 中的工作流程

在 Seq2Seq 中，Attention 机制按照如下流程工作：

1. 准备工作: 编码器处理源句子，得到每个词的隐藏状态 $h_{encoder_1}$, $h_{encoder_2}$, ...。解码器开始工作，有自己的初始隐藏状态 $s_{decoder_0}$。
2. 生成第一个词 "he"：
   1. 计算注意力分数 (Scores): 将解码器的当前隐藏状态 $s_{decoder_0}$（作为Query）与编码器的所有隐藏状态 $h_{encoder_i}$（作为Keys）进行比较，使用点积来计算相似度。这会得到一组分数 $e_1, e_2, ...$。
   2. 计算注意力分布 (Distribution): 将这些分数通过一个 Softmax 函数，将其转换成一个概率分布 $α_1, α_2, ...$。这些 $α$ 值就是注意力权重，它们的和为1。在这个例子中，"il" 对应的权重最高。
   3. 计算注意力输出 (Output): 用这些注意力权重 $α_i$ 去对编码器的隐藏状态 $h_{encoder_i}$（作为Values）进行加权求和，得到一个注意力输出向量（也叫上下文向量 $a_t$）。这个向量选择性地聚合了源句子中当前最相关的信息。
   4. 生成预测: 将这个注意力输出向量 $a_t$ 与解码器的当前隐藏状态 $s_{decoder_0}$ 拼接起来，然后通过一个全连接层和Softmax来预测出目标词 "he"。

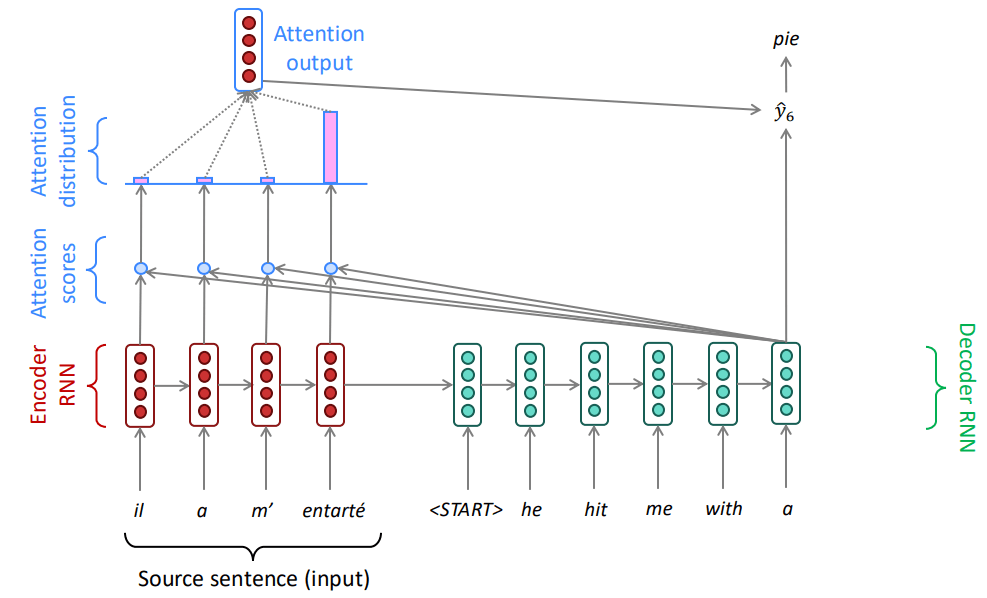
这个过程在解码器的每一步都会重复。例如，在生成 "hit" 时，解码器会用它新的隐藏状态 $s_{decoder_1}$ 再次去计算注意力，此时它可能会更关注源句中的 "entarté" (hit with a pie)。这样，解码器在生成每个词时，都能动态地聚焦于源句子中最相关的部分。

$d.$ 数学表达

上面的工作流程可以用如下的数学公式描述与表达：

• 编码器隐藏状态: $h_1, ..., h_N$
• 解码器在时间步 $t$ 的隐藏状态: $s_t$
• 注意力分数：$e_{ti} = \text{score}(s_t, h_i)$
• 注意力分布：$α_t = \text{softmax}(e_t)$
• 注意力输出 (上下文向量): $a_t = \sum _{i=1} ^{N} α_i^t h_i$
• 最终预测: $y_t = [a_t;s_t]$

$e.$ 注意力机制的优势

在注意力机制中，信息不再需要通过单一的固定向量传递，解码器可以直接访问源句子的所有信息。任何两个词之间的交互距离都变成了 $O(1)$，因为通过注意力机制，它们可以直接交互。

同时，注意力的核心计算是矩阵乘法，非常适合在GPU上并行处理，大大提高了效率。

但是，注意力计算的复杂度是 $O(n^2)$，其中 $n$ 是序列长度，因为需要计算每对词之间的关系。对于非常长的序列，这可能成为性能瓶颈。

$f.$ 注意力机制的泛化

注意力不仅仅是用于 Seq2Seq 模型的技术，它是一种通用的深度学习思想：给定一组向量值 (Values) 和一个向量查询 (Query)，注意力是一种计算值的加权和的技术，而这个权重取决于查询。

我们可以更进一步提出$QKV$框架:

• 查询 (Query): 代表你当前的需求或上下文（例如，解码器的隐藏状态）。
• 键 (Keys): 与值（Values）一一对应，用来和查询（Query）计算相似度（注意力权重）。
• 值 (Values): 真正包含信息的向量。
• 流程：Query 和每个 Key 计算相似度得到权重，然后用权重对相应的 Value 进行加权求和。

这个加权和是对信息的一种选择性总结，而查询 (Query) 决定了要关注哪些信息。它提供了一种方法，可以根据某个上下文（Query），将任意一组向量（Values）压缩成一个固定大小的表示。

9. 门控制单元

虽然理论上普通 RNN 可以捕捉长期依赖，但在实际训练中非常困难。门控制单元（Gated Recurrent Units）的设计目标就是让模型拥有更持久的记忆力，从而更容易地学习到数据中的长期规律。它通过引入“门控机制”来实现这一点，这些“门”可以学习在每个时间步控制信息的流动。

GRU 的核心是更新门 (Update Gate) 和重置门 (Reset Gate)，其关键流程如下：

1. 生成“候选新记忆”：根据当前输入 $x_t$ 和过去的记忆 $h_{t-1}$ 来创造一个新的、临时的记忆 $\tilde{h}_t$。$\tilde{h}_t$ 是对当前时间步信息的总结，可以看作是“提议”要更新的记忆内容。
2. 重置门：$rt$ 决定了过去的记忆 $h_{t-1}$ 在多大程度上可以用来计算“候选新记忆” $\tilde{h}_t$。
   • $r_t$ 接近 1 时，会充分考虑过去的记忆。
3. 更新门：更新门 $zt$ 决定了最终要保留多少过去的记忆 $h_{t-1}$，以及要接受多少“候选新记忆” $\tilde{h}_t$。
   • $z_t$ 接近 1 时，最终的记忆 $h_t$ 会更多地来自于 $z_t \circ h_{t-1}$，也就是更多地保留旧记忆。
4. 最终隐藏状态生成：$h_t = (1 − z_t) \circ \tilde{h}_t + z_t \circ h_{t−1}$，也就是根据更新门的“建议”，将旧记忆和新记忆组合起来，形成当前时间步最终的记忆 $h_t$。

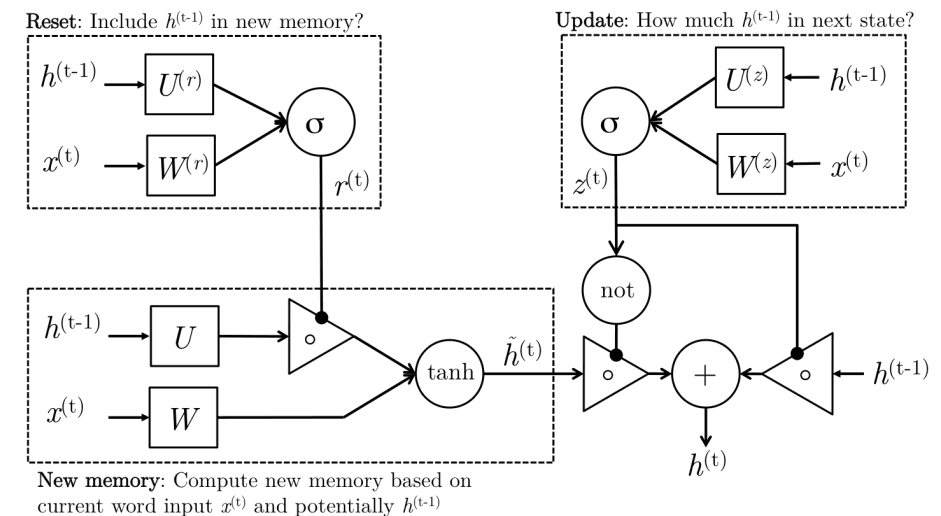
其对应公式如下：

1. $z_t = σ(W^{(z)}x_t + U^{(z)}h_{t−1})$ (更新门)
2. $r_t = σ(W^{(r)}x_t + U^{(r)}h_{t−1})$ (重置门)
3. $\tilde{h}_t = tanh(r_t \circ Uh_{t−1} + Wx_t)$ (候选新记忆)
4. $h_t = (1 − z_t) \circ \tilde{h}_t + z_t \circ h_{t−1}$ (最终隐藏状态)

10. 长短期记忆网络

长短期记忆网络（Long-Short-Term-Memories, LSTM）的核心思想与 GRU 类似，但具体流程有所不同。

LSTM 引入了一个非常重要的概念：细胞状态 (Cell State, $ct$)。可以把它想象成一条独立的“记忆传送带”，信息可以在上面直流，只做一些微小的线性修改。这使得长期记忆的保存变得非常容易。

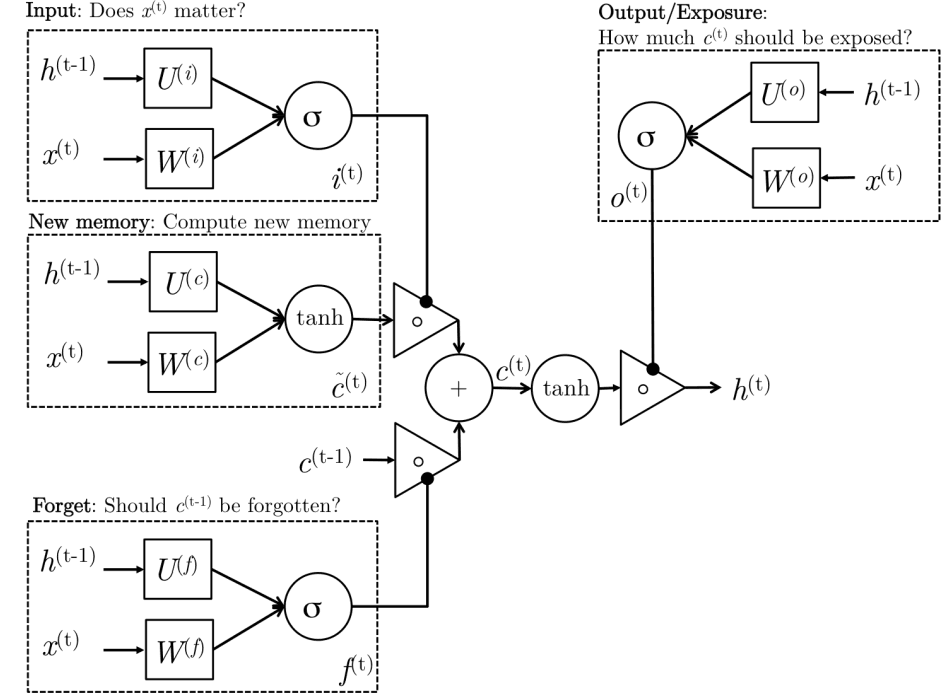
LSTM 主要由三个门组成：输入门、遗忘门和输出门。其关键流程如下：

1. 遗忘门：决定要从细胞状态 $c_{t-1}$（长期记忆）中丢弃哪些信息。它会查看当前输入 $x_t$ 和前一刻的隐藏状态 $h_{t-1}$，然后对 $c_{t-1}$ 中的每一部分信息输出一个 0 到 1 之间的数字。
   • 1 表示“完全保留”，0 表示“完全丢弃”。
2. 输入门与候选新记忆：决定了要向细胞状态中存入哪些新信息：
   1. 首先，$\tilde{c}_t$ 和 GRU 中的一样，创建一个“候选新记忆”。
   2. 然后，输入门 $i_t$ 决定这个候选记忆 $\tilde{c}_t$ 中有哪些部分是重要的、值得被存入长期记忆 $c_t$ 的。
3. 生成最终记忆单元：根据遗忘门和输出门的结果更新长期记忆。

其对应公式如下：

1. $i_t = σ(W^{(i)}x_t + U^{(i)}h_{t−1})$ (输入门)
2. $f_t = σ(W^{(f)}x_t + U^{(f)}h_{t−1})$ (遗忘门)
3. $o_t = σ(W^{(o)}x_t + U^{(o)}h_{t−1})$ (输出门)
4. $\tilde{c}_t = \text{tanh}(W^{(c)}x_t + U^{(c)}h_{t−1})$ (候选新记忆单元)
5. $c_t = f_t \circ c_{t−1} + i_t \circ \tilde{c}_t$ (最终记忆单元)
6. $h_t = o_t \circ \text{tanh}(c_t)$ (最终隐藏状态)