发表于 更新于 分类于 ， 本文字数： 153 阅读时长 ≈ 1 分钟

\(11.4\)树的旋转

  The formal definition of rotation is:

  • rotateLeft(G): Let x be the right child of G. Make G the new left child of x.

  • rotateRight(G): Let x be the left child of G. Make G the new right child of x.

  As in the picture, it means:

  • \(RotateLeft(G)\): G moves left, promote its right child in the only natural way.(Promoting P means P is the new parent of G.)
  • \(RotateRight(P)\): P moves right, promote its left child in the only natural way.

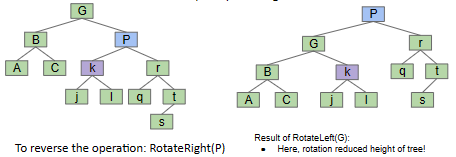
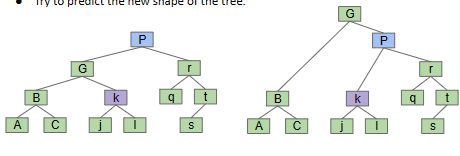
  We can implement these operations by following codes: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private Node rotateLeft(Node h) {
    // assert (h != null) && isRed(h.left);
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    return x;
}

// make a right-leaning link lean to the left
private Node rotateLeft(Node h) {
    // assert (h != null) && isRed(h.right);
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    return x;
}