数据科学基础概念

1. 稀疏矩阵

$a.$ 引入

在数据科学的许多问题中，我们处理的矩阵本质上都是稀疏的：矩阵中绝大多数元素都是零，只有少数非零元素。比如下面两个典型例子：

1. 图（Graphs）：在表示图结构时，一种主要方法是使用邻接矩阵（Adjacency Matrix）。如果节点 $i$ 和节点 $j$ 之间有一条边，那么矩阵中 $(i, j)$ 位置的元素就为非零值。在许多现实世界的图中（比如社交网络），一个节点通常只与少数其他节点直接相连，所以其邻接矩阵会非常稀疏。
2. 自然语言处理（Free Text Modeling）：在处理文本时，常用的一种模型是“词袋模型”（Bag of Words）。我们用一个巨大的向量来表示每一篇文档，向量的每个维度对应词汇表中的一个词，其值表示该词是否在文档中出现（或出现了多少次）。由于一篇文档通常只包含所有可能词汇中的一小部分，因此，由这些文档向量构成的“词-文档共现矩阵”通常也是高度稀疏的。

对于这些矩阵，使用稠密矩阵显式地存储大量的零并让它们参与运算，既浪费内存又浪费计算资源。因此，当矩阵中含有大量零元素时，我们应该利用这一特性来减少内存消耗并加速计算。

从纯数学的角度来看，稀疏矩阵的行为与稠密矩阵完全相同（矩阵乘法、求逆等运算的定义和规则是一样的）。它们本质上是一种计算工具。

$b.$ 坐标格式稀疏矩阵

表示稀疏矩阵最自然的方式就是用一个 (row, col, val) 元组的列表。因为我们知道只有极少数位置有非零值，这种格式让我们只表达存在的条目，所有未指定的条目都默认为零。

在坐标格式 (Coordinate, COO) 中，我们使用三个一维数组来定义一个矩阵：

• values: 存储所有非零元素的值。
• row_indices: 存储这些非零元素对应的行索引。
• col_indices: 存储这些非零元素对应的列索引。

这三个数组的长度相等，都等于矩阵中非零元素的数量 nnz。除了这三个数组，我们还需要额外存储矩阵的维度（行数 m 和列数 n）。

例如，下面这个矩阵：

可以用COO表示为：

• values = [2, 4, 1, 3, 1, 1]
• row_indices = [1, 3, 2, 0, 3, 1]
• column_indices = [0, 0, 1, 2, 2, 3]

COO 格式对元素的顺序没有要求。你可以按任何顺序存储它们。

然而，COO 格式不适合查找或访问矩阵中的元素。比如要查找 A[i,j] 的值，必须线性扫描整个数组，检查是否有任何 (row, col) 对匹配 (i, j)，时间复杂度为 $O(nnz)$。

$c.$ 压缩稀疏矩阵

为了解决 COO 格式查找效率低下的问题，压缩稀疏矩阵 (Compressed Sparse Column, CSC) 明确地维持了非零元素的列主序排列：

• CSC 对 column_indices 数组的定义做了改变。它不再是一个长度为 nnz 的数组，而是一个长度为 $n+1$（$n$ 是矩阵的列数）的指针数组。这个数组的每个元素指向 values 和 row_indices 数组中每一列的起始位置。

例如，前面的矩阵：

在 CSC 中表示如下：

• values = [2, 4, 1, 3, 1, 1] (按列主序排列)
• row_indices = [1, 3, 2, 0, 3, 1] (对应 values 的行索引)
• column_pointers = [0, 2, 3, 5, 6] (列指针)

通过引入这些表示，我们可以快速访问整列数据：

• 第 0 列的数据范围是 [column_pointers[0], column_pointers[1])，也就是 [0, 2)。所以第 0 列的 values 是 [2, 4]，对应的 row_indices 是 [1, 3]。
• 第 1 列的数据范围是 [column_pointers[1], column_pointers[2])，也就是 [2, 3)。所以第 1 列的 values 是 [1]，对应的 row_indices 是 [2]。

以此类推。column_pointers 数组有 $n+1$ 个元素，最后一个元素 column_pointers[n] 的值等于 nnz。这样我们总能用 column_pointers[i]:column_pointers[i+1] 来获取第 i 列的所有数据。

$d.$ 稀疏矩阵的计算优势

以最常见的矩阵向量乘法 $Ax$ 为例：

• 如果 $A$ 是稠密矩阵，计算需要 $O(mn)$ 次操作。
• 如果 $A$ 是稀疏矩阵（以 COO 格式为例），我们可以使用如下的优化算法：
  1. 初始化结果向量 $y$ 为全零。
  2. 对于 $A$ 中的每一个非零元组 $(i, j, v)$，执行 $y[i] = y[i] + x[j] \cdot v$

这个算法只遍历所有非零元素一次，所以操作次数为 $O(nnz)$，这是一个巨大的性能提升。

2. 图表示

$a.$ 邻接字典

我们一般使用邻接字典 (Adjacency dictionary) 的结构表示图，这样我们不仅可以方便地得到一个节点的所有相邻节点，还可以快速查询某一条边是否存在。前者通过List实现，后者通过在List中存储字典结构实现。

例如，对下面的图：

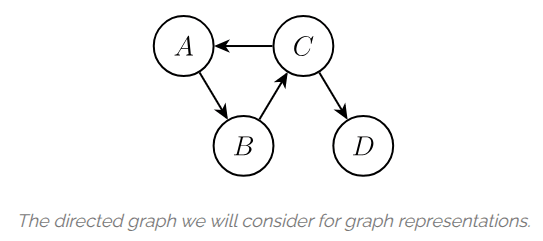
我们可以如下表示：

adj_dict = {"A": {"B":1.0}, "B":{"C":1.0}, "C":{"A":1.0, "D":1.0}, "D":{}}

$b.$ 邻接矩阵

邻接矩阵使用 $A\in \mathbb{R}^{\mid V \mid \times \mid V \mid}$（其中 $V$ 是节点的个数）来表示图结构。这样做的好处是可以直接用这个矩阵进行矩阵乘法等高效率的运算。

由于图大部分都是稀疏的，因此我们使用稀疏矩阵来表示图。例如上面的例子使用 CSC 表示如下：

values = [1,1,1,1]
row_indices = [1, 2, 0, 3]
col_indices = [0, 1, 2, 4, 4]

$c.$ 代码整理(homework)

class Graph:
    def __init__(self):
        """ Initialize with an empty edge dictionary. """
        self.edges = {}

    def add_edges(self, edges_list):
        for a, b in edges_list:
            if a not in self.edges:
                self.edges[a] = {}
            if b not in self.edges:
                self.edges[b] = {}
            self.edges[a][b] = 1
        return self

import scipy.sparse as sp

def adjacency_matrix(g):
    nodes_list = sorted(g.edges.keys()) 
    num_nodes = len(nodes_list)
    node_to_idx = {node: i for i, node in enumerate(nodes_list)}

    row_indices = []
    col_indices = []
    data = []

    for source_node, neighbors in g.edges.items():
        for target_node in neighbors:
            row_indices.append(node_to_idx[target_node])
            col_indices.append(node_to_idx[source_node])
            data.append(1)

    A = sp.coo_matrix((data, (row_indices, col_indices)), shape=(num_nodes, num_nodes))
    return A, nodes_list