决策树

1. 简介

决策树是一种用于分类和回归（比如预测房价）的非线性方法。它的核心结构就像一棵树，包含两种节点：

内部节点 (Internal nodes)：每个内部节点都会对一个特征进行测试，并根据测试结果决定走向哪个分支。通常一次只测试一个特征。
叶节点 (Leaf nodes)：树的最末端，它会给出一个最终的预测结果，比如样本属于哪个类别 $h(x)$ 。

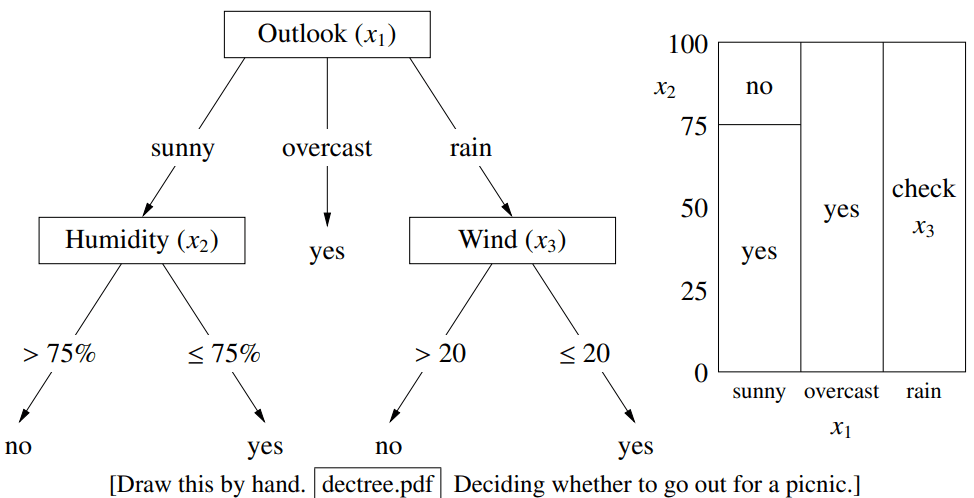
alt text

和线性分类器是用一条直线（或超平面）来划分空间不同，决策树通过一系列与坐标轴平行的“切分”，把整个特征空间划分成一个个“小方块”（矩形区域）。每个“小方块”对应一个叶节点和一个预测结果。这使得它同时适用于类别型和数值型特征。

2. 决策树构建

构建决策树通常采用一种贪心、自顶向下的递归算法：

def GrowTree(S):
    # We say the leaves are pure
    if all(yi == C for i in S for some class C):
        return new leaf(C)
    else:
        # Choose best splitting feature j and splitting value β (*)
        j, beta = choose_best_split(S)
        
        # Or you could use ≤ and >
        S_left = {i for i in S if X[i][j] < beta}
        S_right = {i for i in S if X[i][j] >= beta}
        
        return new node(j, beta, GrowTree(S_left), GrowTree(S_right))

算法中的最佳划分可以用一个成本函数 $J(S)$ 来衡量。我们的目标是最小化切分后子节点成本的加权平均值：

\mathrm{Weighted\_Avg\_Cost}=\frac{\lvert S_{\text{left}}\rvert\,J\bigl(S_{\text{left}}\bigr)+\lvert S_{\text{right}}\rvert\,J\bigl(S_{\text{right}}\bigr)}{\lvert S_{\text{left}}\rvert+\lvert S_{\text{right}}\rvert}

我们采用熵 (Entropy) 的概念来计算成本函数。熵的相关概念如下：

惊喜 (Surprise): 某个事件发生的“惊喜度”是 $-\log_2(p)$ ，其中 $p$ 是该事件发生的概率。概率越小，事件发生时带来的“惊喜”或“信息量”就越大。
熵 (Entropy): 一个集合 $S$ 的熵，是该集合中随机抽取一个样本，其类别所带来的平均惊喜度：

H(S) = - \sum p_C \log_2(p_C)

其中 $p_C$ 是类别 $C$ 在集合 $S$ 中所占的比例。

我们使用熵来选择最佳切分。具体做法是选择能带来最大信息增益的切分：

计算切分前的熵 $H(S)$ 。
计算切分后子节点熵的加权平均值 $H_{\text{after}} = \frac{|S_l|H(S_l) + |S_r|H(S_r)}{|S|}$ 。
则切分的信息增益 $H(S) - H_{\text{after}}$ 。

最大化信息增益，就等同于最小化切分后的加权平均熵 $H_{\text{after}}$ 。因为熵是严格凹函数，信息增益总是非负的。它能很好地区分不同切分的优劣，避免了误分类率的那个问题。

切分的具体方法如下：

对于类别型特征: 如果有多个值，可以进行多路切分（每个值一个分支）或二元切分（将值分为两组）。
对于数值型特征:
1. 将节点中所有样本按该特征值进行排序。
2. 尝试在每两个不相等的相邻值之间进行切分。
3. 一个聪明的技巧: 在扫描排序好的列表时，我们不需要每次都重新计算熵。当我们把切分点从左向右移动一个位置时，仅仅是将一个样本从“右集合”移动到“左集合”。熵的更新可以在 $O(1)$ 时间内完成。这使得对数值型特征寻找最佳切分点的过程非常高效。

3. 决策树回归

我们前面所讲的是使用决策树进行分类，而决策树也可以用来解决回归问题。

决策树回归创建的是一个分段常数回归函数 (piecewise constant regression fn)：决策树会将整个数据空间划分成一个个“小方块”（由叶节点定义），在每个“小方块”区域内，所有数据点的预测值都是同一个常数。

在回归树中，叶节点存储的值不再是类别，而是落入该叶节点的所有训练样本的目标值 $y$ 的平均数：

\mu_S=\frac{1}{\lvert S\rvert}\sum_{i\in S}y_i

在回归树中，我们使用方差 (Variance) 作为成本函数 $J(S)$ ：

J(S)=\operatorname{Var}\bigl(\{y_i\}_{i\in S}\bigr) =\frac{1}{\lvert S\rvert}\sum_{i\in S}\bigl(y_i-\mu_S\bigr)^2,

这个公式衡量的是一个节点内所有样本 $y$ 值的离散程度。如果一个节点内所有样本的 $y$ 值都完全相同，那么方差就是0，成本也为0。因此，分裂的目标是选择一个特征和分裂点，使得分裂后的两个子节点的方差加权平均值最小。

4. 早停

基础的决策树算法会不停地分裂节点，直到每个叶节点都变得“纯净”（即只包含同一类别的样本）。但我们不一定非要这样做，有时候提前停止分裂会是更好的选择。这种方法也叫预剪枝 (Pre-pruning)。

提前停止的原因如下：

限制树的深度: 为了让预测速度更快。
限制树的大小: 当处理非常大的数据集时，一颗完整的树可能会变得异常庞大和复杂。
防止过拟合: 这是最主要的原因。如果一棵树生长得过于完美，以至于每个叶节点都完全纯净，它很可能学习到了训练数据中的噪声和偶然特征，导致在新的、未见过的数据上表现很差。
处理噪声或重叠的分布: 当数据本身有噪声，或者不同类别的数据在特征空间中本来就有很大重叠时，强行追求纯净的叶节点必然会导致过拟合。这时的决策树会像一个 1-近邻 (1-NN) 分类器，对单个训练点非常敏感。更好的做法是提前停止，让叶节点里包含一组近邻点，然后通过投票决定结果，这更像一个 k-近邻 (k-NN) 分类器，模型会更稳健。

我们可以选择如下的条件作为选择停止的条件：

下一次分裂带来的熵减或者误差降低不够大。（但讲义指出这个方法有风险，因为可能某次分裂收益小，但后续分裂收益大。所以后剪枝通常更好）。
节点中大部分样本都属于同一个类别。这可以处理异常值和类别重叠的情况。
节点包含的训练点太少。尤其是在大数据集上，为很少的几个点去分裂意义不大。
节点代表的特征空间的边长已经非常小了。再细分可能没有意义。
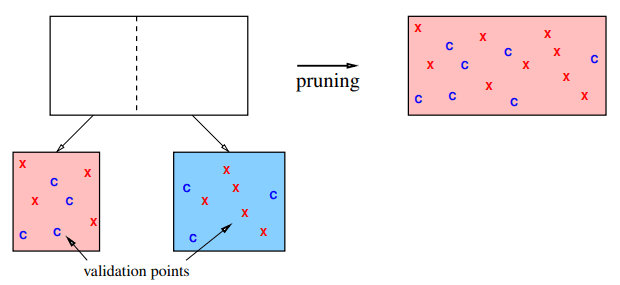
使用验证集 (Use validation) 来比较。这是最慢但最有效的方法：每次分裂前，都在一个独立的验证集上测试，看这次分裂是否真的能降低验证误差。

5. 后剪枝

为了避免过拟合，有一种通常比早停更有效的方法：后剪枝 (Post-pruning)。后剪枝的做法是：先让决策树生长得稍微“过大”一些，然后再用验证集的数据来评估，剪掉那些对验证集性能没有提升甚至有损害的分支。这样做避免了预剪枝“目光短浅”的问题。

我们不需要每次都从整个树中验证数据点，如果使用得当的方法，这个评估的过程可以变得非常快：

首先，将所有验证数据点在完整的、未剪枝的树上完整地跑一次。
对于每一个验证数据点，记录下它最终落在了哪个叶节点。
这样，每个叶节点都会关联一个列表，里面是所有落入该节点的验证数据点。
现在，当我们虑是否要剪掉某一个分裂时（如，合并叶节点 $A$ 和叶节点 $B$ 成为父节点 $P$ ），完全不需要关心树的其他部分。我们只需要关注那些落在叶节点 $A$ 和叶节点 $B$ 里的验证点。
我们只需要局部地计算误差变化：
- 剪枝前：叶节点 $A$ 对它里面的验证点有一个预测，叶节点 $B$ 对它里面的验证点也有一个预测。计算这两个节点总共正确分类了多少验证点。
- 剪枝后：叶节点 $A$ 和叶节点 $B$ 里的所有验证点现在都属于父节点 $P$ 。父节点 $P$ 会给出一个统一的预测。用这个新预测计算总共正确分类了多少验证点。
比较剪枝前后的正确数量。如果剪枝后正确分类的验证点变多了（即验证误差降低了），就执行剪枝。这个计算非常快，因为它只涉及少量数据点的重新归类。

alt text

6. 多元分类

标准的决策树在分裂节点时，每次只针对一个特征创建一个与坐标轴平行的分裂，如 $x_1 < 10$ 或 $x_2 > 5$ ，这些边界都是水平或垂直的。而多元分裂则是创建非轴对齐的 (non-axis-aligned) 分裂，它在一次分裂中会同时考虑多个特征。这种分裂通常是一个线性组合，例如 $3x_1 + 2x_2 > 5$ ，它的决策边界是一条斜线：

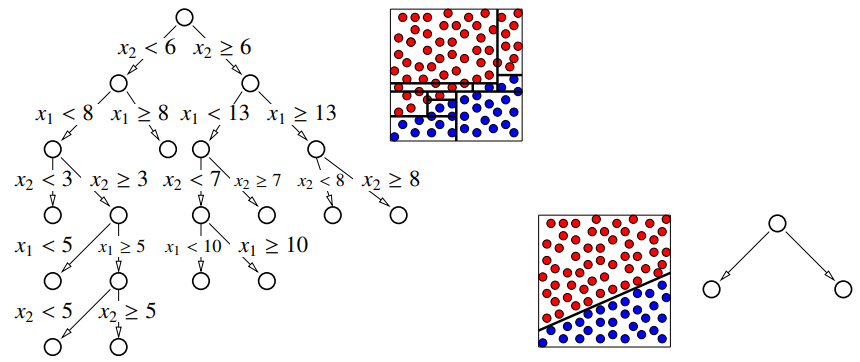
alt text

为了实现这种斜线决策边界，在每个节点，我们可以用其他的分类算法来寻找一个最优的分割超平面，如支持向量机，逻辑回归或高斯判别分析。通过这种方式，决策树允许这些线性分类器以一种层级化的方式组合起来，从而找到非线性的决策边界。

多元分类可能获得一个分类效果更好的分类器，但是也会导致规则的可解释性变差与速度变慢，对此我们可以用前面讲解的特征收缩方法，为每个节点选择合适的特征。

7. 集成学习

决策树有很高的方差：训练数据的微小变化可能会导致生成一棵完全不同的树。假设我们把训练数据随机分成两半，用每一半数据分别训练一棵决策树，这两棵树的结构可能差异巨大，尤其是当它们在根节点的第一次分裂就选择了不同的特征时，后续的整个结构可能就完全不同了。

为了解决这个问题，我们可以采用求平均的方法，通过“平均”许多不同决策树的答案来显著降低模型的方差

想象从某个分布中生成随机数。只生成一个数，它的不确定性可能很高。但如果生成 $n$ 个随机数并取它们的平均值，这个平均值的方差会降为原来的 $\frac{1}{n}$ 。

在机器学习中，我们称那些比随机猜测略好的算法为弱学习器 (weak learner)。集成学习就是将许多弱学习器组合起来，形成一个强大的强学习器 (strong learner)。

集成模型在预测结果时，将一个测试点交给群体中的所有 $T$ 个学习器，然后综合它们的结果：

回归问题: 取所有学习器输出的平均值或中位数。
分类问题: 进行多数投票 (majority vote)，或者平均所有学习器的后验概率，然后选择概率最高的类别。

学习器群体的构建方法主要有以下几种：

Bagging (套袋法): 这是最常用的方法之一。从一个训练集中进行有放回的随机抽样，创建出许多个略有不同的子训练集，然后在每个子训练集上训练一个学习器（例如决策树）。
随机森林 (Random Forests): Bagging的一种特殊形式，在构建决策树时进一步增加了随机性。

集成学习有以下的注意事项：

基学习器应具有低偏差。例如，使用深度决策树，因为它们能很好地拟合训练数据，即使它们因此过拟合。
**基学习器的高方差和过拟合是可以接受的！**集成学习的重点就是通过平均来消除方差。每个学习器可能以自己独特的方式过拟合，但当把它们平均起来时，这些随机的、方向各异的错误会相互抵消。
学习器的数量通常不是需要仔细调整的超参数。学习器的数量越多，方差就降得越低，模型性能就越好。唯一的限制是计算时间：我们是在用时间换取性能。

8. 套袋法

Bagging(Bootstrap AGGregatING) 是一种通用的、随机化的方法，其目的是从同一个训练数据集中创建出许多个不同的学习器，然后将这些学习器的结果“聚合”起来，以获得比单个学习器更好的性能。

该方法对 k-近邻 (k-NN) 算法的效果不佳，甚至可能会轻微地降低其性能。

Bagging 的整体流程如下：

Bootstrap (自助采样法)：这是 Bagging 的第一个核心步骤，也是创建不同学习器的关键。假设我们有一个包含 $n$ 个数据点的训练集。为了创建一个新的子训练集，我们从原始数据集中进行 $n'$ 次有放回的随机抽样（通常 $n'=n$ ）。

如果抽样次数 $n'$ 和原始样本量 $n$ 相等，那么平均而言，一个子训练集大约会包含原始数据中 63.2% 的独立数据点。（剩下的约 36.8% 从未被抽中的数据被称为 “袋外数据” (Out-of-Bag, OOB)，它们可以被用作一个天然的验证集来评估模型性能

Aggregating (聚合)：我们重复 Bootstrap 过程 $T$ $T$ 次，就会得到 $T$ $T$ 个不同的子训练集。然后我们在这 $T$ $T$ 个子训练集上分别训练出 $T$ $T$ 个学习器。然后，我们将这 $T$ $T$ 个学习器的预测结果进行聚合来得到最终的输出。
- 如果一个数据点在一个子训练集中被抽中了 $j$ 次，那么在训练对应的学习器时，这个点的权重就是 $j$ 。这在效果上等同于数据集中有 $j$ $j$ 个完全相同的点挤在一起。
  - 对于决策树: 在计算信息增益时，这个点的权重被视为 $j$ 。
  - 对于SVM: 如果这个点违反了分类间隔，它会产生 $j$ 倍的惩罚项。
  - 对于回归: 在计算损失函数时，这个点会产生 $j$ 倍的损失值。

9. 随机森林

$a.$ 基本算法

Bagging 方法通过对样本进行自助采样来构建多棵树。但这样做还不够好，因为 Bagging 创建出的多棵决策树之间，结构可能仍然非常相似。假如我们的数据集中有一个特别强的预测特征，那么几乎每一个通过自助采样得到的子样本中，这个强特征都很可能存在。因此，在构建决策树时，几乎每一棵树的根节点都会选择这个最强的特征来进行第一次分裂。这会导致树的整体结构非常相似。

为了解决上述问题，随机森林在 Bagging 的基础上，引入了第二次随机，其目标是强制降低树与树之间的相关性。

随机森林在构建决策树的过程中，当对某一个节点进行分裂时，不再是从全部 $d$ 个特征中寻找最优分裂点，而是遵循以下步骤：

从全部 $d$ 个特征中，随机抽取一个包含 $m$ 个特征的子集 ( $m < d$ )。
只在这个 $m$ 个特征的子集中，寻找最优的分割点。
剩下的 $d - m$ 个特征，在当前这个节点的分裂决策中被完全忽略。
对于树的每一个节点，都重复进行一次全新的、独立的特征抽样。

这里的 $m$ 是随机森林的一个关键超参数，它控制了随机性的强度。有一些经验法则可以作为不错的起始值：

分类问题: $m \approx \sqrt{d}$
回归问题: $m \approx \frac{d}{3}$

这里的第二次随机，也体现了偏差-方差的权衡：更小的 $m$ 值意味着更强的随机性：树与树之间的相关性更低。但是，这也意味着在每个节点，算法被限制了选择范围，可能无法使用到那个节点上“真正”最好的特征，这会增加单棵树的偏差。随机森林的精髓在于，它愿意牺牲一点单棵树的准确性（略微增加偏差），来换取整个森林中树的巨大多样性（不相关性）。最终，通过对大量不相关的、性能尚可的树的结果进行平均，总体的方差被极大地降低了，从而获得一个偏差低、方差也低的强大模型。

随机森林方法的优点如下：

预测精度极高，是目前最强大的通用机器学习算法之一。
通常，增加树的数量（几百甚至几千棵）可以持续降低测试误差（因为更多的树能更好地降低方差），不容易过拟合。

但是随机森林方法也有如下问题：

速度慢：训练成百上千棵深度决策树的计算成本很高。
失去了可解释性：模型变成了一个“黑箱”。我们无法像解释单棵决策树那样，直观地向别人解释随机森林的决策逻辑。

$b.$ 随机化分裂类型

除了随机选择特征，我们还可以引入更多随机性：在每个节点，不只局限于轴对齐的分割，而是生成 $s$ 个随机的多元分裂（如，随机的斜线、随机的二次曲线），然后从这 $s$ 个随机生成的分裂中选择最好的一个。

决策树

1. 简介

2. 决策树构建

3. 决策树回归

4. 早停

5. 后剪枝

6. 多元分类

7. 集成学习

8. 套袋法

9. 随机森林

a.a.a. 基本算法

b.b.b. 随机化分裂类型

Comments

$a.$ 基本算法

$b.$ 随机化分裂类型