决策理论

在我们前面讲解的 SVM 分类器中，我们试图找到一个明确的边界（超平面）来分隔不同类别的数据。但现实世界中，数据往往是模糊和重叠的。这就引出了概率分类器的需求：我们不再给出一个“是”或“否”的确定性答案，而是给出一个属于某个类别的概率。

1. 前置概念

我们使用贝叶斯定理来知道我们的决策。首先定义如下的概念：

决策规则 (Decision Rule) $r(x)$ ：一个分类器，它将特征向量 $x$ 映射到一个类别（比如1或-1）。
风险 (Risk) $R(r)$ ：一个决策规则 $r$ 的总风险，定义为在所有数据上损失的期望值：

R(r) = E[L(r(X), Y)]

贝叶斯决策规则 (Bayes Decision Rule) $r^\star$ ：能够使总风险 $R(r)$ 最小化的最优决策规则。
损失函数 (Loss Function) $L(\hat{y}, y)$ ：当预测类别为 $\hat{y}$ 、而实际类别为 $y$ 的惩罚。

我们先只讨论二元分类问题。根据贝叶斯公式，可以如下展开 $R(r)$

\begin{aligned} R(r) &= E\big[L(r(X),Y)\big] \\[4pt] &= \sum_{x}\Big(L(r(x),1)\,P(Y=1\mid X=x) + L(r(x),-1)\,P(Y=-1\mid X=x)\Big)\,P(X=x) \\[6pt] &= P(Y=1)\sum_{x}L(r(x),1)\,P(X=x\mid Y=1) + P(Y=-1)\sum_{x}L(r(x),-1)\,P(X=x\mid Y=-1). \end{aligned}

这里的 $\sum_{x}L(r(x),1)\,P(X=x\mid Y=1)$ 和 $\sum_{x}L(r(x),-1)\,P(X=x\mid Y=-1)$ 可以看作是不同类别概率的权重。

然后我们推导 $r^\star$ 。我们的目标是最小化损失函数。

当我们预测 $r(x)=1$ 时，有：

\begin{aligned} \mathrm{Loss}_A &= L(1,1)\,P\bigl(Y=1\mid X=x\bigr) + L(1,-1)\,P\bigl(Y=-1\mid X=x\bigr)\\[4pt] &= L(1,-1)\,P\bigl(Y=-1\mid X=x\bigr) \end{aligned}

可以看出，我们的期望损失是“把-1错判为1的代价”乘以“真实情况是-1的概率”。

同理得预测 $r(x)=-1$ 时的损失：

\mathrm{Loss}_B=L(-1,1)\,P\bigl(Y=1\mid X=x\bigr)

当损失函数是非对称的 (即 $L(1,-1) \neq L(1,-1)$ ) 时，为了让损失函数最小，可以得到如下决策策略：

r^\star(x)= \begin{cases} +1, & \text{if }\; L(-1,1)\,P(Y=1\mid X=x) > L(1,-1)\,P(Y=-1\mid X=x),\\[6pt] -1, & \text{otherwise.} \end{cases}

当损失条件是对称的时，我们只需要比较 $P\bigl(Y=-1\mid X=x\bigr)$ 和 $P\bigl(Y=1\mid X=x\bigr)$ 的大小，此时决策策略变为 选择后验概率最大的那个类别。

2. 连续分布

前面的推导是基于离散值进行的，下面我们介绍用于连续值特征（比如身高、体重等可以取任意数值的特征）的方法。

$a.$ 连续概率基础知识

对连续概率分布，有如下公式：

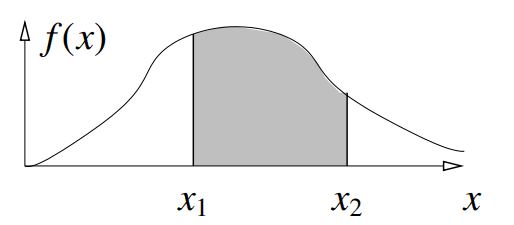
alt text

$P\bigl(X\in[x_1,x_2]\bigr)=\int_{x_1}^{x_2} f(x)\,dx$

$\int_{-\infty}^{\infty} f(x)\,dx=1$

$\mathbb{E}[g(X)]=\int_{-\infty}^{\infty} g(x)\,f(x)\,dx$

$\mu=\mathbb{E}[X]=\int_{-\infty}^{\infty} x\,f(x)\,dx$

$\sigma^{2}=\mathbb{E}\bigl[(X-\mu)^2\bigr]=\mathbb{E}[X^2]-\mu^{2}$

$b.$ 贝叶斯决策

和离散状况一样，我们比较经过先验概率加权后的值 $f(X|Y=1)P(Y=1)$ 和 $f(X|Y=-1)P(Y=-1)$ 。我们在图中作出两者图像，图像的交点就是贝叶斯决策边界：

alt text

同样的，我们展开 $R(x)$ ：

\begin{aligned} R(r) &= E\big[L(r(X),Y)\big] \\[4pt] &= P(Y=1)\int L(r(x),1)\,f_{X\mid Y=1}(x)\,dx \\[4pt] &\quad + P(Y=-1)\int L(r(x),-1)\,f_{X\mid Y=-1}(x)\,dx. \end{aligned}

由于贝叶斯决策选择的是损失函数最小的部分，因此使用贝叶斯决策的风险计算为：

\begin{aligned} R\bigl(r^\star\bigr) &= \int \min_{y=\pm 1} L(-y,y)\,f_{X\mid Y=y}(x)\,P(Y=y)\,dx \end{aligned}

3. 分类器种类

分类器一般分为下面三种类型：

$a.$ 生成模型

生成模型 (Generative Models) 试图去理解数据是如何“生成”的。它会为每一个类别都学习一个独立的概率分布模型。它不只是想区分两个类别，而是想完整地描绘出每个类别下数据的全貌。

这个模型的具体工作流程如下：

假设分布形式：我们首先要做一个假设，比如“我认为患癌病人的某项指标 $x$ 服从高斯分布（正态分布），不患癌病人的指标也服从一个（不同的）高斯分布”。
拟合参数：我们拿出所有类别为 $C$ 的训练样本，然后用这些样本去估计这个类别的高斯分布的参数（比如均值和方差）。这样，我们就得到了似然函数 $f(x|Y=C)$ 。
估计先验概率：我们计算训练数据中每个类别 $C$ 的样本所占的比例，作为先验概率 $P(Y=C)$ 。
使用贝叶斯定理：现在我们有了似然 $f(x|Y=C)$ 和先验 $P(Y=C)$ ，我们就可以使用贝叶斯定理计算出后验概率 $P(Y=C|x)$ 。
做出决策：如果使用0-1损失，我们就选择后验概率 $P(Y=C|x)$ 最大的类别 $C$ 。这等价于选择使 $f(x|Y=C) \cdot P(Y=C)$ 最大的那个类别。

生成模型学习的是特征 $X$ 和标签 $Y$ 的联合概率分布 $P(X, Y)$ 。因为它知道了所有变量的完整模型，所以它不仅能用来预测 $P(Y|X)$ ，还能用来计算 $P(X)$ ，甚至能用来生成新的数据点 $(x, y)$ 。

$b.$ 判别模型

判别模型 (Discriminative Models) 不关心数据是怎么生成的，它只关心如何区分它们。它的目标是直接找到一个模型来预测后验概率 $P(Y|X)$ 。

判别模型直接建立一个函数，输入是 $x$ ，输出就是 $P(Y|X)$ 。

判别模型只对条件概率 $P(Y|X)$ 进行建模，它不关心 $P(X)$ 或 $P(X, Y)$ 。它的唯一目标就是预测目标变量 $Y$ 。

$c.$ 直接寻找决策边界

这是最直接的方法。它既不关心数据生成过程，也不关心概率。它唯一的目标就是找到一个函数 $r(x)$ （即决策边界），能把不同类别的数据点分开 ，并直接对决策函数 $r(x)$ 进行建模。

SVM是这种思想的典型代表。它致力于在两类数据之间找到一个“最宽的街道”，然后把决策边界放在街道的中央。

4. 高斯判别分析

$a.$ 前置知识

高斯分布的定义如下：

X\sim\mathcal{N}(\mu,\sigma^{2}):\qquad f(x)=\frac{1}{(\sqrt{2\pi}\,\sigma)^{d}}\exp\!\left(-\frac{\lVert x-\mu\rVert^{2}}{2\sigma^{2}}\right)

其中 $\mu$ 和 $x$ 是向量， $\sigma$ 是标量。

$b.$ 二次判别分析

在二次判别分析 (Quadratic Discriminant Analysis, QDA) 中，我们假设每个类别的分布是高斯分布，并定义如下的分数函数：

Q_C(x)=\ln\Big((\sqrt{2\pi})^{d}\,f_{X\mid Y=C}(x)\,\pi_C\Big) = -\frac{\lVert x-\mu_C\rVert^{2}}{2\sigma_C^{2}} - d\ln\sigma_C + \ln\pi_C

这里的系数 $(\sqrt{2\pi})^{d}$ 是为了和正态分布的分母抵消。

假设我们只有两个类别 $C$ 和 $D$ ，那么我们的贝叶斯决策为：

r^\star(x)= \begin{cases} C, & \text{if }\; Q_C(x)-Q_D(x)>0,\\[6pt] D, & \text{otherwise.} \end{cases}

注：这里考虑的是损失函数对称的情况。

决策函数为 $Q_C(x)-Q_D(x)$ ，贝叶斯决策边界为 $\lbrace x: Q_C(x)-Q_D(x)=0 \rbrace$ 。

我们使用贝叶斯公式计算后验概率：

P\bigl(Y=C\mid X=x\bigr)=\frac{f_{X\mid Y=C}(x)\,\pi_C}{f_{X\mid Y=C}(x)\,\pi_C+f_{X\mid Y=D}(x)\,\pi_D}

而 $e^{Q_C(x)} = (\sqrt{2\pi})^{d}\,f_{X\mid Y=C}(x)\,\pi_C$ ，于是：

\begin{aligned} P\bigl(Y=C\mid X=x\bigr) &= \frac{e^{Q_C(x)}}{e^{Q_C(x)}+e^{Q_D(x)}} \\[4pt] &= \frac{1}{1+e^{\,Q_D(x)-Q_C(x)}} \\[4pt] &= s\bigl(Q_C(x)-Q_D(x)\bigr) \end{aligned}

其中：

s(\gamma)=\frac{1}{1+e^{-\gamma}}

这里的 $s$ 被称为逻辑函数或 Sigmoid 函数。

对于多类别问题，我们只需要选择 $\arg\max_{C}Q_C(x)$ 的类别 $C$ 即可。

$c.$ 线性判别分析

我们在 QDA 的基础上添加更强的假设：我们不仅假设每个类别的分布是高斯分布，还假设所有类别的高斯分布具有完全相同的方差/协方差矩阵。

基于这个新的假设，我们再次计算 $Q_C(x)-Q_D(x)$ ：

\begin{aligned} Q_C(x)-Q_D(x)\ &=\ \left(-\frac{\lVert x-\mu_C\rVert^{2}}{2\sigma^{2}} - d\ln\sigma + \ln\pi_C\right) - \left(-\frac{\lVert x-\mu_D\rVert^{2}}{2\sigma^{2}} - d\ln\sigma + \ln\pi_D\right) \\[6pt] &=\ \frac{1}{2\sigma^{2}}\bigl(\lVert x-\mu_D\rVert^{2}-\lVert x-\mu_C\rVert^{2}\bigr) \\[6pt] &=\ \frac{1}{2\sigma^{2}}\bigl((\lVert x\rVert^{2}-2x\cdot\mu_D+\lVert\mu_D\rVert^{2})-(\lVert x\rVert^{2}-2x\cdot\mu_C+\lVert\mu_C\rVert^{2})\bigr) \\[6pt] &=\ \frac{1}{2\sigma^{2}}\bigl(2x\cdot\mu_C-2x\cdot\mu_D+\lVert\mu_D\rVert^{2}-\lVert\mu_C\rVert^{2}\bigr) \\[6pt] &=\ \frac{(\mu_C-\mu_D)\cdot x}{\sigma^{2}}-\frac{\lVert\mu_C\rVert^{2}-\lVert\mu_D\rVert^{2}}{2\sigma^{2}}. \end{aligned}

这个表达式现在是 $x$ 的线性函数，可以写成 $w \cdot x + α$ 的形式。它具有如下特征：

决策边界: 决策边界是 $w \cdot x + α = 0$ ，这是一个超平面。
后验概率: 和 QDA 类似，后验概率 $P(Y = C|X = x)$ 仍然可以用 Sigmoid 函数表示，但输入变成了线性的 $s(w \cdot x + α)$ 。

特别地，当两个类别的先验概率相等时，决策边界方程为：

(\mu_C-\mu_D)\cdot\left(x-\frac{\mu_C+\mu_D}{2}\right)=0

这正是质心法的决策函数。因此，当先验概率相同时，LDA 的决策边界是连接两个类别中心的线段的垂直平分线。分类器会把一个新数据点 $x$ 分给离它更近的那个质心。

对于多类别问题，我们只需要选择 $\arg \max _C \frac{\mu_C\cdot x}{\sigma^{2}}-\frac{\lVert\mu_C\rVert^{2}}{2\sigma^{2}}+\ln\pi_C$ 的类别 $C$ 即可。

5. 最大似然估计

$a.$ 基本概念

在实践中，我们使用最大似然估计 (Maximum Likelihood Estimation, MLE) 来计算在 QDA 或 LDA 中需要的参数 $πC$ , $µC$ , $σ²C$ 。

MLE 的核心思想如下：给定一组观测到的数据，我们反过来问：什么样的模型参数，能让这组数据出现的概率（似然）最大？我们就用这组“最可能”的参数作为我们对模型真实参数的估计。

$b.$ 高斯分布的最大似然估计

现在我们详细讲解怎么为一系列数据点 $X_1, X_2,\dots,X_n$ 拟合一个最佳的高斯分布。

对于连续分布，任何单个数据点 $X_i$ 出现的概率其实是零。这似乎让“最大化出现概率”变得没有意义。在连续函数中，我们转而使用概率密度函数 $f(x)$ 的值来代表“似然性”。一个点的概率密度越大，我们可以认为它在该分布下出现的“可能性”就越高。

我们假设所有样本点是独立同分布的 (IID)，那么观测到所有这些点的联合似然，就是它们各自似然的乘积：

L(µ, σ) = f(X_1) f(X_2)\dots f(X_n)

这个式子不太好进行计算，因此我们取对数：

\begin{aligned} \ell(\mu,\sigma) &= \ln f(X_1) + \ln f(X_2) + \dots + \ln f(X_n) \\[4pt] &= \sum_{i=1}^n\left(-\frac{\lVert X_i-\mu\rVert^{2}}{2\sigma^{2}} - d\ln\sqrt{2\pi} - d\ln\sigma\right) \end{aligned}

根据 MLE 原理，我们需要计算出让 $\ell(\mu, \sigma)$ 最大的参数值，因此我们令参数梯度为0：

{\mu}\ell = 0, \quad \frac{\partial\ell}{\partial\sigma} = 0

得：

\nabla_{\mu}\ell = \sum_{i=1}^n \frac{X_i-\mu}{\sigma^2} = 0 \Rightarrow\quad \hat{\mu} = \frac{1}{n}\sum_{i=1}^n X_i

\frac{\partial\ell}{\partial\sigma} = \sum_{i=1}^n \frac{\lVert X_i-\mu\rVert^{2}-d\sigma^{2}}{\sigma^{3}} = 0 \Rightarrow\quad \hat{\sigma}^{2} = \frac{1}{dn}\sum_{i=1}^n \lVert X_i-\mu\rVert^{2}

这样，要估计类别 $C$ 的高斯分布的均值 $µ_C$ 和方差 $σ²_C$ ，我们只需要使用训练数据中所有属于类别 $C$ 的点，然后计算这些点的样本均值和样本方差即可。注意到 $\sigma ^ 2$ 的计算中需要 $\mu$ ，这里我们使用通过样本估计的 $\mu$ 来计算。

$c.$ QDA 与 LDA 的样本参数

QDA 的样本均值 $\hat{\mu}_{C}$ 、样本方差 $\hat{\sigma^2_{C}}$ 都是直接基于样本数据计算即可。QDA 的先验概率计算如下：

\hat{n}_C=\frac{n_C}{n}

对于 LDA，由于我们假设方差均等，我们不能只计算某个类的方差，也不能简单地把所有数据混在一起算一个总方差，而是计算池化类内方差 (pooled within-class variance)：

\hat{\sigma}^2 \;=\; \frac{1}{dn}\sum_{C}\sum_{i: y_i = C}\lVert X_i - \hat{\mu}_C\rVert^{2}

$\sum_{i: y_i = C}\lVert X_i - \hat{\mu}_C\rVert^{2}$ 对所有属于类别 $C$ 的样本 $i$ 计算到自己类别中心 $\hat{\mu}_C$ 的平方。这部分计算的是类别 $C$ 内部的总离散程度。(这是“类内 (within-class)”这个词的来源)
我们对所有类别 C 都进行上述计算，然后把结果全部加起来。汇集到一个“池子”里。 (这是“池化 (pooled)”这个词的来源)

决策理论

1. 前置概念

2. 连续分布

a.a.a. 连续概率基础知识

b.b.b. 贝叶斯决策

3. 分类器种类

a.a.a. 生成模型

b.b.b. 判别模型

c.c.c. 直接寻找决策边界

4. 高斯判别分析

a.a.a. 前置知识

b.b.b. 二次判别分析

c.c.c. 线性判别分析