生成：Gemini-2.5-pro，整理：fyerfyer

神经网络训练

1. 神经生物学基础

人工神经网络的许多核心概念都源于对生物大脑工作方式的模仿。通过对比生物神经系统，我们可以更深刻地理解人工神经网络的设计哲学。

大脑的基本计算单元是神经元 (Neuron)，它是一个负责处理和传递信息的细胞：

神经元 (Neuron)：大脑和神经系统的基本构成单位，负责思考与通讯。
动作电位 (Action Potential / Spike)：神经元用于与其他神经元交流的电化学脉冲信号。当一个神经元要传递信息时，它会“放电”或发射一个脉冲。
轴突 (Axon)：神经元上负责传出信号的“输出线”，动作电位沿着它传播。
树突 (Dendrite)：神经元上负责接收信号的“输入线”，呈树枝状。
突触 (Synapse)：一个神经元的轴突末梢与另一个神经元的树突相连接的“接头”，是信息传递的关键节点。
神经递质 (Neurotransmitter)：当动作电位到达轴突末梢时，会释放这种化学物质。它穿过突触间隙，与下一个神经元的树突上的受体结合，从而影响下一个神经元的电压，决定其是否也产生一次“放电”。这个过程在1到5毫秒内完成。

可以将我们的人工神经网络与生物大脑进行如下类比：

生物大脑概念	人工神经网络 (ANN) 概念	详细说明
神经元放电频率	单元的输出值	生物神经元的放电是“全或无”的，信息通过放电频率编码（如1000次/秒代表强信号"1"）。这对应ANN中一个节点的连续输出值（如0.9）。
突触强度	连接的权重 (Weight)	生物突触的连接强度决定了其对下游神经元的影响力大小。这直接对应ANN中连接的权重值。
兴奋性/抑制性神经递质	正/负权重	兴奋性递质促进放电，类似正权重；抑制性递质（如GABA）抑制放电，类似负权重。ANN的优势在于权重可以自由地在正负间变化。
输入的时空累加	输入的线性组合	生物神经元整合所有输入信号，当累积电压超过阈值时才放电。这对应ANN中对所有输入进行加权求和（ $\sum w_i x_i$ ）。
放电频率饱和	激活函数 (Sigmoid/ReLU)	生物神经元的放电频率有物理上限（如<1000Hz）和下限(0Hz)。这对应ANN中使用激活函数将输出值压缩到特定范围（如[0, 1]），防止输出无限增大。

2. 学习机制的对比

$a.$ 赫布法则

大脑学习的生物学基础被认为是突触可塑性 (Synaptic Plasticity)，即突触的连接强度是可变的。赫布法则 (Hebb's Rule) 对此做出了经典概括：

"Cells that fire together, wire together."

这意味着，如果一个神经元的放电总是能促使另一个神经元也放电，它们之间的兴奋性连接就会增强。基于赫布法则的算法虽然存在，但其学习速度和效果远不如反向传播。

反向传播是现代神经网络训练的核心算法。然而，它在生物学上的真实性备受质疑。

尽管有一些理论试图解释大脑中可能存在类似反向传播的机制，但这些解释都非常牵强。大脑真正的学习机制至今仍未被完全理解。计算机科学家研究神经生物学是为了获取灵感来改进算法，而神经学家研究ANN则是为了构建数学模型来理解大脑。

3. 训练加速优化

$a.$ 优化算法的选择

批量梯度下降 (Batch GD)：每一步都使用整个训练集来计算梯度。方向准确，但速度慢，内存开销大。
随机梯度下降 (Stochastic GD, SGD)：每一步只用一个随机样本来计算梯度。速度快，但更新方向非常不稳定，“嘈杂”。
小批量随机梯度下降 (Mini-batch SGD)：这是目前最主流的方法，是上述两者的折中。

每次更新使用一个大小为 $b$ （如 $b=256$ ）的小批量数据来计算梯度。

w \leftarrow w - \epsilon \nabla J_{minibatch}(w)

小批量SGD的优势如下:

收敛更稳定快速：通过平均一个小批量样本的梯度，降低了更新的方差（约为纯SGD的 $1/\sqrt{b}$ ），使得收敛路径更平滑。
高效利用硬件：不同样本的梯度计算是独立的，极易在GPU上进行并行化和向量化处理，极大提升计算效率。
优化内存访问：将小批量数据在内存中连续存放，可以高效利用CPU/GPU的缓存，分摊数据加载的开销。训练64个样本的速度可能和训练1个样本相差无几。

下面是一些在实际训练过程的注意事项：
在每个epoch开始前，应随机打乱整个训练集。
确保小批量是训练集的代表性抽样。对于不平衡数据集，可以采用分层采样，确保每个小批量中的类别比例与整体一致。
最佳学习率 $\epsilon$ 与批量大小 $b$ 相关，调整 $b$ 后通常需要重新寻找最佳 $\epsilon$ 。

$b.$ 学习率 $\epsilon$ 的选择

寻找最佳学习率可能非常耗时。一个非常实用的技巧是：使用一小部分随机抽样的训练数据来快速测试和估算一个好的学习率，然后将这个学习率应用到整个训练集上。实践表明，最佳学习率对训练集的大小并不十分敏感。

$c.$ 样本加权方案

神经网络会很快学会常见样本，而对稀有样本学得很慢。加权方案旨在解决此问题：

动机：强制模型关注那些稀有的、或被错误分类的样本。
方法：
- 对于SGD：可以更频繁地从稀有类别中抽样，或者在训练这些样本时使用更大的学习率 $\epsilon$ 。
- 对于Batch GD：在总代价函数中，为来自稀有类别的样本损失赋予更大的权重。

这一方法在处理类别极不平衡的数据时（如罕见病检测）非常有效，可以防止模型“偷懒”只预测多数类。

注意，此方法也可能放大“坏的异常值”（如错误标注的样本）的影响，导致模型学到错误信息，需要谨慎使用。

$d.$ 数据标准化

这是几乎所有情况下都推荐的数据预处理步骤。标准化常用的方法如下：

中心化 (Center)：对每个特征，减去其均值，使其均值为0。
缩放 (Scale)：对每个特征，除以其标准差，使其方差为1。

我们需要标准化的原因如下：

激活函数的有效区域：激活函数（如Sigmoid）的非线性区域通常在输入接近0的地方。标准化使得第一层隐藏单元的输入更容易落在这个有效区域，从而让网络更有效地学习。
改善代价函数的形状：标准化可以改善代价函数海森矩阵的条件数，将一个狭长的“山谷”地形（ill-conditioned）变得更像一个圆形的“碗”（well-conditioned），梯度下降可以更顺畅地走向最低点，从而加速收敛。
公平的正则化：如果使用L2正则化，标准化可以确保对所有特征的惩罚是公平的。

注意：在训练集上应用的任何标准化变换（减去的均值、除以的标准差），之后在验证集和测试集上也必须应用完全相同的变换。

$e.$ 权重初始化

正确的权重初始化对深度网络的训练至关重要。前面讲到了随机初始化权重以打破对称性。但初始值太小会导致梯度消失，太大则会导致梯度爆炸。于是，我们采用下面的权重初始化策略：

基本原则：一个单元的输出方差，应与其输入的方差保持一致。
经验法则 为了实现这一原则，我们设 $\eta_{in}$ $η_{in}$ 为一个单元的输入连接数 (fan-in)，则：
- ReLU 单元: He 初始化。从均值为0，方差为 $2/\eta_{in}$ 的正态分布 $\mathcal{N}(0, 2/\eta_{in})$ 或相应范围的均匀分布中采样。
- tanh 或线性单元: Xavier/Glorot 初始化。从均值为0，方差为 $1/\eta_{in}$ 的正态分布 $\mathcal{N}(0, 1/\eta_{in})$ 或相应范围的均匀分布中采样。

一个神经元的输入越多（fan-in越大），它接收到的信号总和就越大。为了平衡这一点，我们需要让每个输入的权重变得更小一些。所以，初始化的公式通常都包含除以扇入（或其变体）的操作。

对偏置项初始化，有:

隐藏层偏置: 通常初始化为0。
输出层偏置: 一个很好的技巧是，将其设置为能让网络初始输出接近训练数据的平均标签。例如，如果90%的样本是正类，就设置偏置使Sigmoid输出默认为0.9。这可以避免训练初期浪费大量时间去学习这个基本的数据分布。

$f.$ 动量

动量法是一种经典的梯度下降优化算法。它基于如下的直觉：如果之前的梯度方向大致相同，那么当前步伐应该更大。这就像给梯度下降的小球增加了“惯性”，帮助它冲出局部极小值的“小坑”，并在狭长的“山谷”中加速。

动量法的更新规则如下：

维护一个“动量”向量 $m$ ，它累积了过去梯度的指数衰减平均值。

\begin{aligned} m &\leftarrow \beta m - \epsilon \nabla J(w) \\ w &\leftarrow w + m \end{aligned}

其中 $\beta$ 是动量超参数（如0.9），控制“惯性”的衰减率。

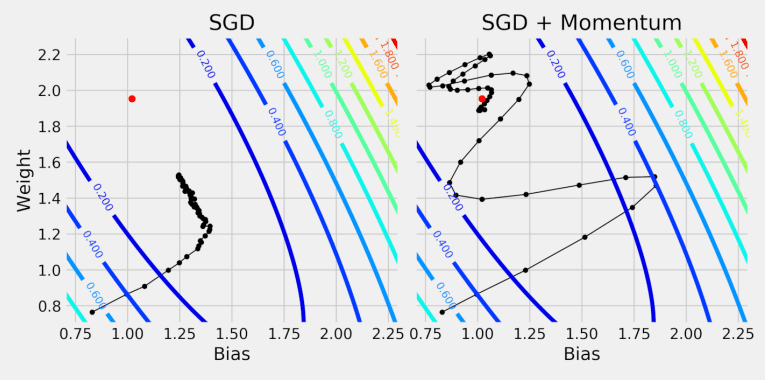
动量法通常能让模型更快地收敛到最优解附近。但其缺点是，由于惯性，它可能会“冲过头”，在最优点附近来回震荡。

把神经网络的代价函数想象成一个复杂的水上乐园滑道。使用带动量的梯度下降法就像一个成功的游泳者，能够利用惯性顺利地滑向终点（局部最小值）。

alt text

神经网络训练

1. 神经生物学基础

2. 学习机制的对比

a.a.a. 赫布法则

3. 训练加速优化

a.a.a. 优化算法的选择

b.b.b. 学习率 ϵ\epsilonϵ 的选择

c.c.c. 样本加权方案

d.d.d. 数据标准化

e.e.e. 权重初始化

f.f.f. 动量

Comments