最大间隔分类器

线性分类器的间隔 (Margin) 是决策边界与离它最近的训练样本点之间的距离。

在最大间隔分类器 (Maximum Margin Classifiers) 中，我们试着让这个间隔尽可能地宽。因为直觉上，一条位于“正中间”的、间隔最大的分界线，对于新出现的数据点会有更好的判断力。因为它没有偏向任何一边，所以更“公平”，也更不容易因为训练数据中微小的扰动而产生巨大的变化。

我们稍微修改一下前面的约束式子，把它进行如下加强：

y_i\,(w\cdot X_i + \alpha) \ge 1,\quad \text{for } i\in\{1,\dots,n\}

而在前面的笔记中，我们知道当 $w$ 为单位向量时， $f(x)=w \cdot x + \alpha$ 可以表示有向距离，这样分类器的间隔就表示为：

$\min_{i}\frac{1}{\|w\|}(w\cdot X_i+\alpha)\ge \frac{1}{\|w\|},\ \forall i$

这样，我们的优化问题就转换为：

\begin{aligned} \min_{w,\alpha}\;&\|w\|^2\\[6pt] \text{s.t.}\;& y_i\,(X_i\cdot w + \alpha)\ge 1,\quad i=1,\dots,n \end{aligned}

这里我们选择优化 $\|w\|^2$ 而不是 $\|w\|$ ，因为 $\|w\|^2$ 是一个处处可导的凸函数，求解起来更为容易。

然后我们看看式子中的“间隔”体现在什么地方。我们在图中作出我们的决策边界 $w\cdot x + \alpha = 0$ 和我们的间隔边界 $w\cdot x + \alpha = 1$ 、 $w\cdot x + \alpha = -1$ ：

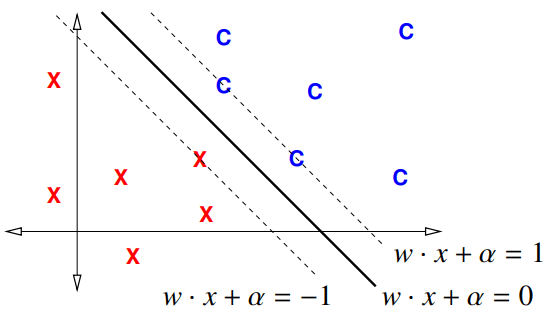
alt text

间隔边界中间的区域的宽度即为 $\frac{1}{\|w\|} \cdot 2$ 。

我们知道，最大间隔分类器的间隔宽度由以下式子决定：

y_i\,(w\cdot X_i + \alpha) \ge 1

而在空间中，实际“支撑”着这个间隔的，是落在间隔边缘上的向量：

y_i\,(w\cdot X_i + \alpha) = 1

如果移动了这些向量中的任意一个，整个最大间隔面都会移动。而移动其他的向量（在间隔范围内）并不会影响间隔面的形状。这些向量被称为支撑向量 (Support Vectors)。

这意味着，最终的最大间隔面仅仅由一小部分支持向量所决定，而与绝大多数其他数据点无关。这为之后我们的一些方法奠定了基础。

这里的解释其实是不严谨的，真正严谨的推导会在 “支持向量机” 这篇文章中详细讲解，这里只提供一个感性的认识。