神经网络

• 39 min read • 7788 words
Tags: Deep Learning Ma-Le
Categories: Machine Learning

生成：Gemini-2.5-pro，整理：fyerfyer

神经网络

1. 简介

a.a. 概述

神经网络 (Neural Networks) 是一种功能强大的非线性模型，可同时用于分类 (Classification) 和回归 (Regression) 任务。

它融合了机器学习中的多个核心概念：

  • 感知机 (Perceptrons): 构成神经网络的基本单元。
  • 线性/逻辑回归: 单个神经元可视为这些模型的扩展。
  • 集成学习 (Ensembles): 复杂的神经网络可看作是大量简单学习器（神经元）的集成。
  • 随机梯度下降 (SGD): 训练神经网络参数的核心优化算法。

与传统方法需要手动设计特征不同，神经网络最革命性的特点之一是能够自动学习特征 (Feature Learning)。它通过组合简单的神经元，将原始数据逐层抽象，最终学习出解决复杂问题所需的高维特征表示。

b.b. 解决 XOR 问题的思路

1969年，Marvin Minsky 和 Seymour Papert 在其著作《感知机》中，指出了一个致命缺陷——异或 (XOR) 问题。

XOR 是一个简单的逻辑运算：

x1x2y
000
011
101
110

当我们将这四个数据点绘制在二维平面上时，会发现它们是线性不可分 (linearly inseparable) 的，即无法用一条直线将类别0和类别1完美分开。由于单个感知机本质上是一个线性分类器，因此它无法解决XOR问题。

一个简单的思路是手动为数据增加一个非线性特征，例如 x1x2x_1x_2。这样，原始的二维数据点就被映射到了三维空间：

x1x2x1*x2y
0000
0101
1001
1110

在新的三维空间中，数据点变得线性可分了。我们可以轻易地找到一个平面（三维空间中的线性分类器）来分离开两个类别：

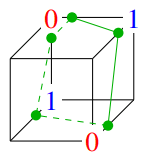
alt text

但这种方法依赖于人工设计特征，不具备通用性。更强大的方法是构建一个多层网络。

  1. 初步想法：将多个线性分类器（感知机）的输出作为后续分类器的输入。
  2. 遇到的问题：线性组合的线性组合，结果仍然是一个线性组合。无论叠加多少层线性分类器，其最终效果都等价于一个单一的线性分类器，因此依然无法解决XOR问题。
  3. 关键补充：非线性激活函数 为了打破线性的限制，我们必须在每一层线性组合之后，引入一个非线性激活函数 (Non-linear Activation Function)。

线性组合 →\rightarrow 非线性激活 →\rightarrow 线性组合 →\rightarrow 非线性激活 →\rightarrow ...

通过这种方式，网络获得了拟合复杂非线性决策边界的能力。一个经典的例子是用多个神经元组合模拟逻辑门来解决XOR问题：

x1⊕x2=(x1 OR x2) AND (x1 NAND x2)x_1 \oplus x_2 = (x_1 \text{ OR } x_2) \text{ AND } (x_1 \text{ NAND } x_2)

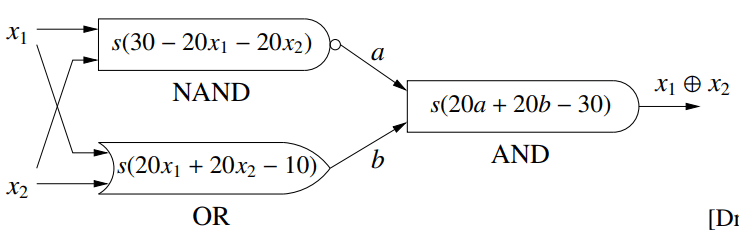
alt text

这里的核心问题是：我们能否设计一个算法，让网络自动学习出这些组合的权重？答案就是反向传播算法。

2. 单隐藏层网络结构

a.a. 整体架构

一个典型的单隐藏层网络由三部分构成：

  1. 输入层 (Input Layer): 接收 dd 维的原始数据向量 x\mathbf{x}。
  2. 隐藏层 (Hidden Layer): 包含 mm 个神经元，负责提取和转换特征。其输出为 mm 维向量 h\mathbf{h}。
  3. 输出层 (Output Layer): 产生 kk 维的最终预测结果 y^\mathbf{\hat{y}}。

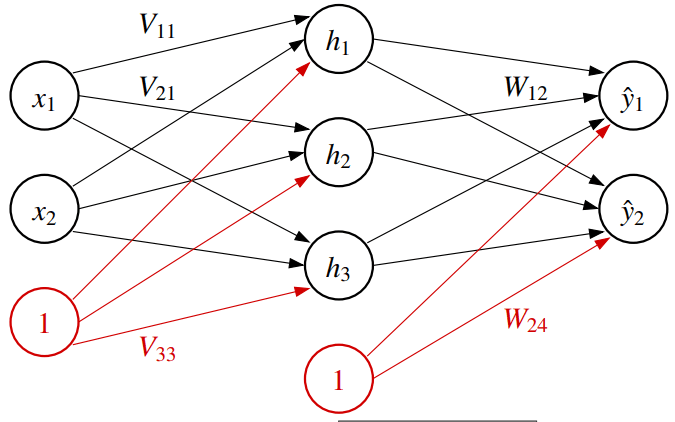
alt text

b.b. 权重矩阵与偏置项

网络的“知识”存储在连接各层神经元的权重中，这些权重被组织成矩阵。

  • 第一层权重 VV: 维度为 m×(d+1)m \times (d+1)，连接输入层和隐藏层。
  • 第二层权重 WW: 维度为 k×(m+1)k \times (m+1)，连接隐藏层和输出层。

为了将偏置项 (bias) 整合进矩阵运算，我们为输入向量 x\mathbf{x} 和隐藏层输出向量 h\mathbf{h} 增加一个恒为1的虚拟维度 (fictitious dimension)。这样，线性运算 Wx+bW\mathbf{x} + \mathbf{b} 就可以被简化为 W′x′W'\mathbf{x'}。

c.c. 前向传播 (Forward Propagation)

前向传播是指数据从输入层流向输出层，并计算出最终预测值的过程。

  1. 计算隐藏层输出 h\mathbf{h}: 首先进行线性组合，然后通过非线性激活函数 ss（例如 Sigmoid 函数）。
h=s1(Vx)\mathbf{h} = s_1(V\mathbf{x})

其中 s1s_1 表示逐元素应用激活函数 ss 后，再为向量末尾追加一个1（作为下一层的偏置项）。对于隐藏层中的第 ii 个神经元：

hi=s(Vi⋅x)h_i = s(\mathbf{V}_i \cdot \mathbf{x})

(Vi\mathbf{V}_i 是权重矩阵 VV 的第 ii 行)

  1. 计算输出层输出 y^\mathbf{\hat{y}}: 将隐藏层的输出 h\mathbf{h} 作为输入，重复上述过程。
y^=s(Wh)\mathbf{\hat{y}} = s(W\mathbf{h})

对于输出层中的第 jj 个神经元：

y^j=s(Wj⋅h)\hat{y}_j = s(\mathbf{W}_j \cdot \mathbf{h})

(Wj\mathbf{W}_j 是权重矩阵 WW 的第 jj 行)

将两步合并，整个网络的计算可以表示为一个高度非线性的函数：

y^=s(Ws1(Vx))\mathbf{\hat{y}} = s(W s_1(V\mathbf{x}))

3.网络训练

a.a. 代价函数

训练的目标是找到最优的权重矩阵 VV 和 WW，使得网络的预测值 y^\mathbf{\hat{y}} 与真实标签 y\mathbf{y} 尽可能接近。

  • 损失函数 (Loss Function) L(y^,y)L(\mathbf{\hat{y}}, \mathbf{y}): 衡量单个样本的预测误差。例如，回归任务常用的均方误差： L(y^,y)=∥y^−y∥2L(\mathbf{\hat{y}}, \mathbf{y}) = \|\mathbf{\hat{y}} - \mathbf{y}\|^2
  • 代价函数 (Cost Function) J(V,W)J(V, W): 衡量网络在整个训练集上的平均误差。 J(V,W)=1n∑i=1nL(y^(xi),yi)J(V, W) = \frac{1}{n} \sum_{i=1}^n L(\mathbf{\hat{y}}(\mathbf{x}_i), \mathbf{y}_i)

b.b. 梯度下降

我们使用梯度下降 (Gradient Descent) 来寻找代价函数的最小值。其核心思想是沿着代价函数梯度的反方向更新权重。

令 w\mathbf{w} 为一个包含网络中所有权重（来自 VV 和 WW）的长向量，更新规则如下：

w←w−ϵ∇J(w)\mathbf{w} \leftarrow \mathbf{w} - \epsilon \nabla J(\mathbf{w})

其中 ϵ\epsilon 是学习率 (Learning Rate)，控制更新的步长；∇J(w)\nabla J(\mathbf{w}) 是代价函数对所有权重的梯度。

c.c. 局部最小值

神经网络的代价函数是非凸 (non-convex) 的，存在许多局部最小值。梯度下降算法可能会陷入一个非最优的局部最小值。不过在实践中，通过精心设计的网络和优化算法，通常能找到一个“足够好”的解。

d.d. 权重初始化与对称性问题

不能将所有权重都初始化为0。如果这样做，隐藏层中的所有神经元在每次迭代时都会计算出完全相同的值和梯度，它们的权重也会以完全相同的方式更新。这种对称性 (Symmetry) 使得多个神经元退化成一个，网络将无法学习复杂的特征。

为了打破对称性，权重必须被初始化为小的随机数。

4.反向传播算法

反向传播是高效计算梯度 ∇J(w)\nabla J(\mathbf{w}) 的核心算法。它本质上是一种动态规划，通过在计算图上反复应用链式法则 (Chain Rule) 来避免重复计算。

a.a. 核心思想

任何复杂的数学表达式都可以表示为一个计算图。反向传播分为两步：

  1. 前向传播: 从左到右计算图中每个节点的值，并缓存结果。
  2. 反向传播: 从右到左计算梯度。核心法则是：某节点的梯度 = 上游传来的梯度 × 本地梯度。

b.b. 分支处理

当一个节点的输出流向多个后续节点时（在神经网络中非常普遍），其总梯度等于所有路径的梯度之和。

∂L∂α=∑i∂L∂yi∂yi∂α\frac{\partial L}{\partial \alpha} = \sum_i \frac{\partial L}{\partial y_i} \frac{\partial y_i}{\partial \alpha}

c.c. 具体流程

反向传播的过程是从后向前，逐层计算梯度。

  1. 计算输出层的误差信号:

首先计算损失函数 LL 相对于网络直接输出 y^\mathbf{\hat{y}} 的梯度 ∇y^L\nabla_{\hat{y}} L。这个梯度是反向传播的起点。

  1. 计算第二层权重 WW 的梯度:

应用链式法则，将来自上一步的误差信号 ∇y^L\nabla_{\hat{y}} L 乘以本地梯度 ∇Wy^\nabla_W \mathbf{\hat{y}}。

∇WL=(∇y^L)⋅(∇Wy^)\nabla_W L = (\nabla_{\hat{y}} L) \cdot (\nabla_W \mathbf{\hat{y}})
  1. 计算隐藏层的误差信号:

将输出层的误差信号 ∇y^L\nabla_{\hat{y}} L 通过权重 WW 反向传播回隐藏层，得到隐藏层的误差信号 ∇hL\nabla_h L。

∇hL=(∇y^L)⋅(∇hy^)=WT(∇y^L)⋅(...)\nabla_h L = (\nabla_{\hat{y}} L) \cdot (\nabla_h \mathbf{\hat{y}}) = W^T (\nabla_{\hat{y}} L) \cdot (\text{...})
  1. 计算第一层权重 VV 的梯度:

使用上一步得到的隐藏层误差信号 ∇hL\nabla_h L，重复步骤2的逻辑，计算 VV 的梯度。

∇VL=(∇hL)⋅(∇Vh)\nabla_V L = (\nabla_h L) \cdot (\nabla_V \mathbf{h})

d.d. 统一的梯度形式

对于三种常见的输出层配置，尽管其激活函数和损失函数形式各异，但最终的梯度形式却惊人地统一：

输出层配置1. 线性 + 均方误差2. Sigmoid + 逻辑损失3. Softmax + 交叉熵
∇WL\nabla_W L2(y^−y)hT2(\mathbf{\hat{y}} - \mathbf{y})\mathbf{h}^T(y^−y)hT(\mathbf{\hat{y}} - \mathbf{y})\mathbf{h}^T(y^−y)hT(\mathbf{\hat{y}} - \mathbf{y})\mathbf{h}^T
∇hL\nabla_h L2WT(y^−y)2W^T(\mathbf{\hat{y}} - \mathbf{y})WT(y^−y)W^T(\mathbf{\hat{y}} - \mathbf{y})WT(y^−y)W^T(\mathbf{\hat{y}} - \mathbf{y})

这种简洁的形式并非巧合。它是精心选择的损失函数（如逻辑损失）的“爆炸梯度”与激活函数（如Sigmoid）的“消失梯度”在数学上抵消的结果，最终留下了 (y^−y)(\mathbf{\hat{y}} - \mathbf{y}) 这个干净、稳定的误差项。

5.梯度消失问题与激活函数

a.a. 梯度消失问题

Sigmoid 函数在输出接近0或1的区域非常平坦，其导数 s′=s(1−s)s' = s(1-s) 趋近于0。在深层网络中，根据链式法则，梯度在反向传播时会与多个接近0的导数连乘，导致梯度信号逐层衰减，最终完全消失。这使得靠近输入层的网络权重无法得到有效更新，训练极其缓慢或停滞。

为了解决梯度消失问题，现代神经网络普遍在隐藏层使用 ReLU (Rectified Linear Unit) 作为激活函数。

  • 定义: r(γ)=max⁡(0,γ)r(\gamma) = \max(0, \gamma)
  • 导数:
r′(γ)={1,γ>00,γ≤0r'(\gamma) = \begin{cases} 1, & \gamma > 0 \\ 0, & \gamma \le 0 \end{cases}

对于所有被激活的神经元（输入>0），其梯度恒为1。这意味着梯度信号可以无衰减地通过这些神经元进行反向传播，极大地缓解了梯度消失问题，使得训练深度网络成为可能。

隐藏层通常使用ReLU，但输出层的激活函数和损失函数需要根据具体任务来专门选择。

任务类型常用激活函数常用损失函数目的/类比
回归线性 (无)均方误差预测连续值 (线性回归)
二分类Sigmoid逻辑损失/交叉熵预测概率，避免输出层梯度消失 (逻辑回归)
多分类Softmax交叉熵预测概率分布，避免输出层梯度消失 (Softmax回归)

b.b. Softmax 函数

Softmax 函数将一个 kk 维的实数向量 a\mathbf{a} 转换为一个 kk 维的概率分布向量 y^\mathbf{\hat{y}}。

y^i=eai∑j=1keaj\hat{y}_i = \frac{e^{a_i}}{\sum_{j=1}^k e^{a_j}}

其输出的所有元素都在 (0, 1) 之间，且总和为1，可解释为输入属于各个类别的概率。

6.神经网络与生物学

人工神经网络的灵感部分来源于生物大脑，但两者在计算风格上有本质区别：

特性CPU (中央处理器)Brain (生物大脑)
处理方式串行 (Sequential)大规模并行 (Massively Parallel)
组件速度纳秒级 (ns)毫秒级 (ms)
容错性脆弱 (Fragile)极强 (Fault-tolerant)
擅长领域精确计算、逻辑规则视觉、语音、联想、模糊问题

大脑的记忆以一种分布式的方式存储在亿万神经元的连接权重中，而非存储在某个特定的神经元里。这使得大脑具有极强的容错能力。训练得当的人工神经网络也具备此特性

Comments

Total words: 7788