最近邻算法

1. 最近邻分类

最近邻分类 (k-NN) 是机器学习中最直观、最简单的算法之一。其核心思想可以用一句老话概括：“物以类聚，人以群分”。

$a.$ 核心思想

给定一个需要预测类别的查询点 (query point) $q$，算法会执行以下操作：

1. 在所有训练数据中，找到离 $q$ 最近的 $k$ 个训练点。
2. “最近”的定义取决于你选择的距离度量 (Distance metric)，例如欧氏距离、曼哈顿距离等。

根据这 $k$ 个最近的邻居，我们可以进行回归或分类：

• 回归 (Regression)：返回这 $k$ 个邻居的标签值的平均值。例如，预测房价时，可以找 $k$ 个最相似的房子，取它们价格的平均值。
• 分类 (Classification)：
  1. 多数投票 (Majority Vote)：返回这 $k$ 个邻居中出现次数最多的类别。
  2. 类别概率直方图 (Histogram of class probabilities)：返回一个各类别的概率分布。例如，如果 $k=10$，其中有 7 个是 A 类，3 个是 B 类，那么模型会预测该点属于 A 类的概率是 70%，B 类的概率是 30%。

类别概率直方图方法试图估计后验概率。但它的精度有限。比如，如果 $k=3$，那么你唯一可能得到的概率就是 $0, 1/3, 2/3,$ 或 $1$。虽然增大 $k$ 可以提高概率的精度，但又可能导致欠拟合 (underfit)。这种方法在拥有海量数据时效果最好。

$b.$ 对参数 $k$ 的理解

参数 $k$ 是一个“平滑”参数，它直接控制了模型的复杂度和决策边界的形状，体现了经典的偏见-方差权衡 (Bias-Variance Trade-off)。

• 当 $k$ 很小 (例如 $k=1$) 时:
  • 模型变得更复杂，决策边界会非常复杂、犬牙交错。
  • 优点：能捕捉到数据的局部、复杂模式 (低偏见)。
  • 缺点：对噪声非常敏感，容易过拟合 (Overfitting) (高方差)。模型过于关注局部细节和噪声，泛化能力差。
• 当 $k$ 很大 (例如 $k=100$) 时:
  • 模型变得更简单，决策边界会非常平滑。决策是基于一个非常大的邻域的“平均特征”做出的。
  • 优点：对噪声鲁棒性好，模型更稳定 (低方差)。
  • 缺点：可能忽略数据的局部细节，容易欠拟合 (Underfitting) (高偏见)。模型因为它“看得太宽”，反而“看不清细节”了。
• 合适的 $k$:
  • 一个合适的 $k$ 可以在复杂度和光滑度之间取得平衡。
  • 它能够生成一个既能捕捉数据大趋势，又能忽略噪声的决策边界，接近理想的贝叶斯决策边界 (Bayes decision boundary)。
  • 通常，理想的 $k$ 值取决于你数据的密度。数据越密集，最优的 $k$ 值通常也越大。

$c.$ 理论保证

尽管 k-NN 算法很简单，但它有很强的理论支持。

• 定理 1 (Cover & Hart, 1967): 当训练样本数量 $n o infinity$ (趋近于无穷大) 时，1-NN 分类器的错误率满足： $\text{错误率} < 2B - B^2$ 其中 $B$ 是贝叶斯风险 (Bayes Risk)，即在给定数据分布下，任何分类器所能达到的理论最低错误率。

这个定理非常惊人。它告诉我们，即使是如此简单的 1-NN 算法，其长期错误率也最多不会超过最优分类器错误率的两倍。这为这个简单算法的有效性提供了强有力的保证。一个重要的前提是，训练点和测试点都必须独立地从同一个概率分布中抽取。

• 定理 2 (Fix & Hodges, 1951): 当 $n \rightarrow \infty$，$k \rightarrow \infty$，并且 $k/n \rightarrow 0$ 时，k-NN 分类器的错误率会收敛到贝叶斯风险 $B$。

这意味着，在满足特定条件下，k-NN 是贝叶斯最优 (Bayes optimal) 的。也就是说，只要数据足够多，并且 $k$ 值选择得当，k-NN 最终可以达到理论上的最佳性能。

• $n \rightarrow \infty$：需要海量数据。
• $k \rightarrow \infty$：需要考虑足够多的邻居来消除噪声，得到稳定的估计。
• $k/n \rightarrow 0$：$k$ 的增长速度必须远慢于 $n$。这保证了所选的邻居仍然是“局部”的，从而能反映查询点附近的真实数据分布。

2. 最近邻搜索算法

k-NN 的思想很简单，但如何高效地找到那 $k$ 个最近的邻居是一个关键问题。

$a.$ 穷举 k-NN 算法 (Exhaustive k-NN)

这是最直接的暴力搜索方法。给定一个查询点 $q$，我们：

1. 遍历所有 $n$ 个训练点，计算它们与 $q$ 之间的距离。
2. 维护一个数据结构（如最大堆），始终保存着到目前为止所见过的 $k$ 个最短距离。

我们可以使用一个大小为 $k$ 的最大堆对这一过程进行优化。堆顶元素是当前 $k$ 个最近邻中，距离查询点 $q$ 最远的那个。当遍历到一个新点，若其距离比堆顶元素更近，则移除堆顶，插入新点。对于大的 $k$ 值，这能显著提高效率。

• 训练时间: $O(0)$。k-NN 是“懒惰学习”(Lazy Learning) 算法，训练阶段仅存储数据。
• 查询时间: $O(nd + n \log k)$。
  • $O(nd)$：遍历 $n$ 个点，每次计算距离的复杂度是 $O(d)$（$d$ 是数据维度）。
  • $O(n \log k)$：遍历 $n$ 个点，每次更新堆的复杂度是 $O(\log k)$。

暴力搜索在数据量大时太慢。我们需要通过预处理 (preprocess) 训练点，来获得亚线性 (sublinear) 的查询时间（即比 $O(n)$ 更快）。

$b.$ Voronoi 图的概念

Voronoi 图 (Voronoi Diagrams) 是一种将空间划分为多个区域的数据结构，非常适合解决最近邻问题。

给定一个点集 $X$，对于其中任意一个点 $w \in X$，它的 Voronoi 单元 (Voronoi cell) Vor(w) 定义为：

点 $w$ 的 Voronoi 单元是空间中所有点的集合，这些点离 $w$ 的距离比离 $X$ 中任何其他点 $v$ 的距离都要近或相等。可以把它想象成每个点 $w$ 在空间中的“势力范围”或“领地”。

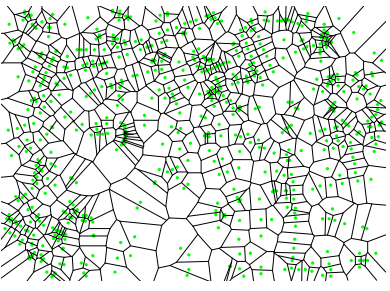
Voronoi 图的大小（如顶点数量）的理论上界是 $O(n^{\lceil d/2 \rceil})$，随着维度 $d$ 指数级增长。但在低维（如2D, 3D）下，其大小通常接近 $O(n)$。

$c.$ 使用 Voronoi 图进行搜索

使用 Voronoi 进行搜索的具体流程如下：

1. 预处理：为训练点构建 Voronoi 图。
2. 点定位 (Point Location)：给定一个查询点 $q$，高效地确定 $q$ 落在哪个点的 Voronoi 单元里。一旦找到这个单元，其对应的中心点就是 $q$ 的最近邻。

为了实现快速的点定位，我们需要第二个数据结构。在 2D 环境下，可以构建一个梯形图 (trapezoidal map)。

梯形图的构建方法如下：从 Voronoi 图的每一个顶点开始，向上和向下各发射一条垂直的“射线”，直到它撞上另一条 Voronoi 图的边为止。这些垂直线和原始边一起，把平面分割成了一系列简单的梯形。在完成分割后，我们可以建立一个类似二叉搜索树的搜索结构（一个有向无环图 DAG），通过回答一系列“在分割线的左边/右边？”或“在分割边的上面/下面？”的是/非问题，来快速定位查询点所在的梯形。

构建 Voronoi 图和梯形图的预处理时间是 $O(n \log n)$，而查询时间可以达到极快的 $O(\log n)$。

然而，标准的 Voronoi 图根据定义，只能找到1个最近邻 (1-NN)。虽然存在 k 阶 Voronoi 图，但因其尺寸爆炸且缺乏可靠软件而无人使用。

Voronoi 图是一个理解最近邻搜索问题的绝佳概念。它在低维（2-5维）下对 1-NN 查询非常高效，但在更高维度或需要 k>1 的邻居时，k-d 树是更好的选择。

$d.$ k-d 树的概念

k-d 树（k-dimensional tree）是专门用于最近邻搜索的“决策树”。

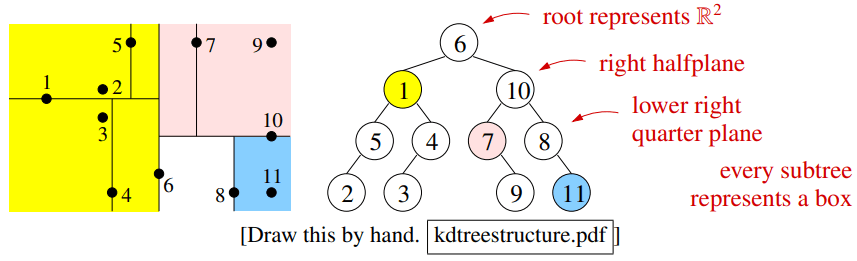
k-d 树通过递归地将空间用与坐标轴平行的超平面进行分割，从而构建一棵二叉树。

在选择分裂维度时，一般选择当前盒子中宽度最大的那个维度进行分裂，以使得划分出的盒子尽可能“方正”。

分裂值的选择方法如下：

• 中位数：选择该维度上所有点的中位数作为分裂点。这能保证树的平衡，深度为 $O(\log n)$。
• 中点：在盒子在该维度上的中点进行分裂。这能让盒子形状更好，但可能导致树不平衡。

$e.$ 使用 k-d 树进行搜索

使用 k-d 树搜索的核心思想是剪枝 (Pruning)。通过维护一个“迄今为止找到的最近邻居”的记录，来避免搜索那些不可能包含更近邻居的树节点（盒子）。具体的状态量如下：

• $w$：迄今为止找到的最近邻居。
• $r$：查询点 $q$ 到 $w$ 的距离。这定义了一个以 $q$ 为中心，$r$ 为半径的“搜索球”。
• $\text{dist}(q, B)$：查询点 $q$ 到一个盒子 $B$ 的最短可能距离。如果 $q$ 在盒内，距离为0；否则是到盒子边界的距离。

在搜索时，如果要探索的下一个盒子 $B$ 满足 $dist(q, B) \ge r$，那么整个盒子 $B$ 以及它下面的所有子树就不需要再探索了，可以直接“剪掉”。

k-d 树搜索的完整流程如下：

1. 从根节点开始，递归地向下搜索，找到包含查询点 $q$ 的叶子节点，将该叶子节点中的点作为当前最近邻 $w$。
2. 开始回溯。在回溯的每一步：
   • 如果当前节点中的点比 $w$ 更近，则更新 $w$。
   • 检查当前节点的另一个子节点所对应的盒子。如果该盒子与以 $q$ 为中心、半径为 $r$ 的搜索球相交（即 $\text{dist}(q, B) < r$），则必须进入那个子树，从那里开始一个新的递归搜索。
3. 回溯到根节点后，算法结束，$w$ 即为最近邻。

$e.$ 近似搜索

在最坏情况下（特别是高维空间），k-d 树可能需要访问树中的每一个节点，性能退化到比暴力搜索还慢。

这时，我们可以进行近似搜索，通过允许一点点误差（$\epsilon > 0$）来解决这个问题。剪枝条件放宽为 $(1 + ϵ) \text{dist}(q, B) \ge r$。这使得算法可以更早、更激进地剪枝。

在实践中，特别是高维空间，近似搜索的速度可以比精确搜索快 10 到 100 倍，而找到的点通常也已经足够好了。