伪逆与神经网络生成方法优化

1. 伪逆

$a.$ 定义

伪逆是一个矩阵的广义逆。常规的逆矩阵 $X^{-1}$ 只对可逆的方阵存在。而伪逆 $X^{+}$ 对任何形状的矩阵都存在。

如果一个 $n \times d$ 的矩阵 $X$ 的紧凑 SVD 分解是 $X = UDV^T$ ，那么它的摩尔-彭若斯伪逆 (Moore-Penrose Pseudoinverse) $X^{+}$ 定义为：

X^{T} = VD^{-1}U^T

这是一个 $d \times n$ 的矩阵。

我们对 $X$ 的 SVD 分解取转置：

X^T = (UDV^T)^T=VDU^T

可以看出， $X^{+}$ 就像是 $X$ 的转置 $X^T$ ，但把其中的奇异值 $\delta_i$ 换成了它们的倒数 $\frac{1}{\delta_i}$ 。

$b.$ 重要性质

$XX^{+}=UU^T,\quad X^{+}X=VV^T$

将 $X$ 和 $X^{+}$ 的定义式代入即得。下面我们来分析这个性质。

首先我们先明确正交投影矩阵的两个判断标准：

对称性 (Symmetry): $P = P^T$ 。
幂等性 (Idempotence)： $P^2=P$ 。

先简单阐释这两个标准的来源。幂等性的理解较为简单：我们希望不管投影多少次、投影的结果都是不变的，也就是说不论我们为 $X$ 施加多少次投影变换 $P$ ，结果都是一致的。

然后是对称性。这是对垂直投影的要求：我们希望连接 $X$ 的顶端和其影子 $p$ 的顶端的那条“光线” $e = x - p$ ，必须与“地面” $S$ 完全垂直，也就是与 $S$ 中任意一个向量 $s$ 垂直，也即：

s^T(x - Px) = 0

下面我们来证明当 $P=P^T$ 时，这个式子成立。注意到 $s$ 在 $S$ 上、本身即是一个投影，由 $P$ 的幂等性：

\begin{aligned} s^{T}(x - P x) &= s^{T}x - s^{T}P x,\\[6pt] \Rightarrow\quad s^{T}x &= (P s)^{T}x \qquad\text{(since }s = P s\text{)},\\[6pt] &= s^{T}P^{T}x \qquad\text{(transpose property)},\\[6pt] &= s^{T}P x \qquad\text{(since }P^{T}=P\text{)},\\[6pt] \Rightarrow\quad s^{T}(x - P x) &= s^{T}x - s^{T}P x = s^{T}P x - s^{T}P x = 0. \end{aligned}

而 $U$ 和 $V$ 显然满足这两条性质，因此它们是正交投影矩阵。

而对于 $U$ ，它的列向量张成了 $X$ 的整个列空间，对于任意向量 $z$ ，变换 $UU^T$ 为：

(UU^T)z=U(U^Tz)=U(U\cdot z)

这正是向量投影的定义： $UU^T$ 将输入 $X$ 投影到它的列空间中。同理， $VV^T$ 将输入 $X$ 投影到它的行空间中。从而， $XX^{+}$ 与 $X^{+}X$ 也具有这样的性质。

这一性质说明了 $X$ 和 $X^{+}$ 并非在整个空间上互为逆矩阵，它们只在 $X$ 的行空间和列空间这两个“有效区域”之间才表现出完美的互逆关系。对于任何超出这两个区域的向量分量，这个求逆过程都会伴随着一次投影，也就是一次不可逆的信息损失。这正是伪逆与真正的逆 $A^{-1}$ 的根本区别。

同时这也说明： $XX^{+}$ 在 $X$ 的列空间上是单位映射 (identity map)。也就是说，对于任何在 $X$ 列空间中的向量 $z$ ，有 $XX^{+}z = z$ 。

如果 $X$ 是行满秩 ( $r = n$ )， $X^{+}$ 是一个右逆 ( $XX^{+} = I$ )。
如果 $X$ 是列满秩 ( $r = d$ )， $X^{+}$ 是一个左逆 ( $X^{+}X = I$ )。
如果 $X$ 是一个可逆的方阵 ( $r = n = d$ )，那么 $X^{+} = X^{-1}$ 。这说明伪逆是常规逆的推广。

我们只证明第一条。首先代入 SVD：

\begin{aligned} X^{+}X &= (V\Sigma^{+}U^{T})(U\Sigma V^{T})\\[6pt] &= V\Sigma^{+}(U^{T}U)\Sigma V^{T} \\[6pt] &= V\Sigma^{+}\Sigma V^{T} \end{aligned}

由于 $X$ 是行满秩，计算对角矩阵 $\Sigma$ 得：

\begin{aligned} \Sigma^{+}\Sigma &= \mathrm{diag}\!\left(\frac{1}{\sigma_1},\dots,\frac{1}{\sigma_d}\right) \,\mathrm{diag}(\sigma_1,\dots,\sigma_d)\\[6pt] &= I_d \end{aligned}

于是：

\begin{aligned} X^{+}X &= V I_d V^{T}\\[6pt] &= V V^{T} \end{aligned}

由于 $V$ 为 $d \times d$ 正交矩阵，于是：

\begin{aligned} X^{+}X &= I_d \end{aligned}

$X^{+}$ 和 $X^T$ 具有相同的四个基本子空间（行空间、列空间、零空间、左零空间）。这意味着 $X^{+}$ 的行空间就是 $X$ 的列空间， $X^{+}$ 的列空间就是 $X$ 的行空间。

这个结论的证明非常简单，只需要知道：

$X$ 的列空间 $C(X)$ 由 $U$ 的前 $r$ 个列向量 $[u_1, ..., u_r]$ 张成。
$X$ 的行空间 $C(X^T)$ 由 $V$ 的前 $r$ 个列向量 $[v_1, ..., v_r]$ 张成。
$X$ 的零空间 $N(X)$ 由 $V$ 的后 $d-r$ 个列向量 $[v_{r+1}, ..., v_d]$ 张成。
$X$ 的左零空间 $N(X^T)$ 由 $U$ 的后 $n-r$ 个列向量 $[u_{r+1}, ..., u_n]$ 张成。

$c.$ 几何直观

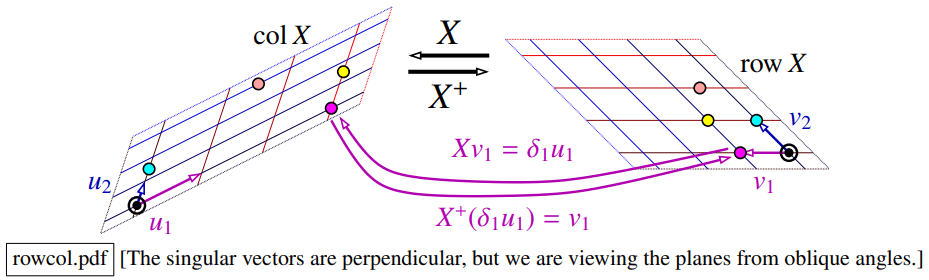
矩阵 $X$ 可以看作一个线性函数，它将它的行空间中的向量一一对应地映射到它的列空间中：

$v_1$ , $v_2$ 是行空间的一组基（右奇异向量）。
$u_1$ , $u_2$ 是列空间的一组基（左奇异向量）。
$X$ 把 $v_i$ 映射为 $\delta_iu_i$ (方向不变，长度缩放 $\delta_i$ 倍)。
$X^{+}$ 把 $u_i$ 映射回 $(1/\delta_i)v_i$ (方向不变，长度缩放 $1/\delta_i$ 倍)。
当我们用 $X$ 作用于一个行空间中的向量，再用 $X^{+}$ 作用于结果时，可以得到原始的向量：

X^{+}(Xv) = v

这就是前面性质中说的“单位映射”。

alt text

$d.$ 在正规方程中的应用

伪逆最重要的应用场景之一就是求解最小二乘中的正规方程：

X^TXw = X^Ty

容易证明：无论 $X^TX$ 是否可逆， $w=X^{+}y$ 永远是方程的一个解。

同时，当正规方程有无穷多解时（ $X^TX$ 不可逆的情况）， $w = X^{+}y$ 是所有解中范数最小的那一个。在机器学习中，一个范数更小的解通常意味着模型更简单，更不容易过拟合，因此这个是一个最稳定的解。

2. 防止过拟合的方法整理

$a.$ 数据增强

当无法获取更多真实数据时，数据增强是一种极其有效的替代方案。例如，对于一张猫的图片，我们可以通过水平翻转、缩放、平移等操作，告诉模型：“你要学会识别的是猫的本质特征，而不是它在图片中的具体位置、方向、光照或颜色。”

数据增强有下面两种思路：

切线传播 (Tangent Propagation) - 基于模型的正则：这是一种更复杂、更“数学化”的方法。它不是直接生成新图片，而是在模型的误差函数中添加一个正则化项。这个正则化项会惩罚“当输入发生微小变换时，模型输出发生剧烈变化”的情况。例如，如果输入图片被平移了0.1个像素，这个正则化项就会阻止模型输出的类别概率发生大的跳变。
- 它的缺点是实现复杂，需要额外的计算开销，并且通常只能处理非常微小的变换。
数据集增强 (Data Set Augmentation) - 基于数据的扩充：这是我们通常所说的数据增强。它直接在训练前或训练中生成新的、经过变换的图像，来扩充数据集。它的实现相对简单，效果非常好，应用广泛。
- 对于随机梯度下降等在线学习算法: 可以在每次将数据点送入模型之前，对其进行一次随机变换。这样，在多轮训练（epochs）中，模型每次看到的同一个原始样本都是略有不同的版本，非常高效。
- 对于批量方法: 可以将每个数据点复制多次，对每个副本独立进行变换，然后用这个扩充后的、更大的数据集进行训练。

通过对误差函数进行泰勒展开来分析微小变换带来的影响，可以从理论上证明：数据增强在效果上等价于向误差函数中添加了一个正则化项，这个等效的正则化项惩罚的是 “网络输出相对于变换的梯度”。

其他方法都比较常见，这里略过。

3. 双下降

生成：ChatGPT 5，整理：fyerfyer

在深度学习的早期发展阶段，研究者普遍秉持一种“控制模型规模”的谨慎态度。这种观念源于两方面的担忧：

神经网络在训练过程中可能会陷入所谓“坏的局部最小值”，从而导致训练误差长期停留在较高水平。
若模型包含过多参数，便极易出现严重的过拟合现象，进而破坏泛化性能。

因此，彼时的主流理论认为：模型应当尽可能保持简洁，以避免损害模型在新数据上的表现。这一思路与统计学中的经典“偏差—方差权衡”高度一致：随着模型复杂度的增加，偏差会下降，但方差随之上升。二者之间的平衡被视为模型选择的核心。

这一理论的具体推导参见前面的 "对机器学习方法的统计证明" 笔记。

然而，伴随计算能力的显著提升与大规模实践经验的积累，人们逐渐意识到，这种担忧在现实场景中并不完全成立。首先，所谓“坏的局部最小值”并非实质性障碍。通常情况下，若模型无法进一步降低训练误差，其根本原因往往不是因陷入恶性最优点，而在于模型容量不足。换言之，约束过严才是性能受限的主要因素。

由此得出的对策十分直接：通过增加网络的宽度或深度来扩展容量。当网络规模足够庞大时，它几乎总能在训练集上达到接近零的误差，即实现对所有训练样本的插值（interpolation）。在这一状态下，模型能够逐点“记忆”数据，从而在训练过程上取得完美的拟合。

在这样的背景下，一个关键问题随之出现：如果模型在训练集上已经能够完全拟合数据，依据传统偏差-方差理论，它在测试集上的表现应当非常糟糕。然而，现代实证研究却揭示出一种显著偏离理论预期的曲线形态。

按照经典理论，若将模型复杂度作为横轴、测试误差作为纵轴绘制曲线，其走势应呈现一个“U”型：当复杂度从低水平逐步提升时，模型能够更好地捕捉真实的规律，偏差下降，测试误差随之降低；但在复杂度超过某一最佳区间后，模型逐步吸收数据中的噪声，方差显著增加，测试误差随之升高。然而，现代实验表明，当模型规模进一步扩大时，测试误差并非持续上升，而是出现再次下降的趋势。曲线表现为：先下降、后上升，再度下降，这一新现象即被称为“双下降”（Double Descent）：

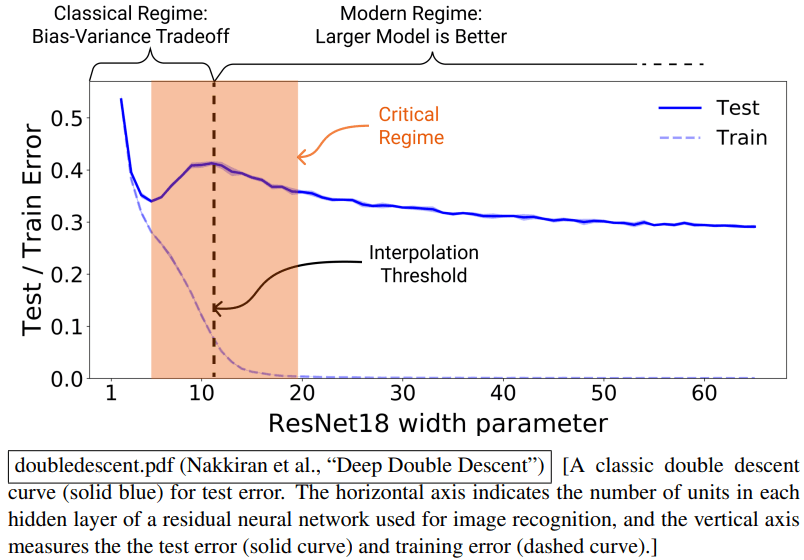
alt text

更具体而言，在模型复杂度逐渐增加的过程中，首先会出现与经典理论一致的阶段：测试误差下降至某一最低点；随后，在复杂度到达所谓的插值阈值（interpolation threshold）时，误差剧烈攀升，形成峰值。此时模型的参数容量刚好足以拟合所有训练点，包括其中的噪声数据或错误标注。由于缺乏更大的空间来调整其内部表示，模型被迫生成一条极不光滑的函数曲线以满足所有约束，其结果是泛化能力显著下降。

然而，在进一步增加模型容量、进入过参数化（over-parameterized）区域之后，情况出现根本改变。此时，能够实现零训练误差的解已不再唯一，而是存在于一个庞大且连续的解空间中。优化算法（例如随机梯度下降）在这些候选解中并非完全无差别地选择，而是由于其隐式偏差，倾向于选择更为“平滑”或“简洁”的解，如权重范数较小的函数形式。因而，冗余参数为模型提供了巨大的“自由度”，从而使得它既能在样本点处精确拟合，又能在整体函数形态上保持近似的平滑与简洁。这一机制有效缓解了由噪声拟合带来的泛化问题。

尤为重要的是，双下降并非神经网络的特例，而是在诸如决策树、带随机特征的线性回归等多种模型中均可观测到的普遍现象。这表明，双下降并不仅是某类神经模型的独有产物，而极有可能是一条更为基本的机器学习原理：它揭示了在高度过参数化情境中，模型复杂性、训练拟合能力与泛化性能之间的一种全新关系。

伪逆与神经网络生成方法优化

1. 伪逆

a.a.a. 定义

b.b.b. 重要性质

c.c.c. 几何直观

d.d.d. 在正规方程中的应用