特征收缩方法

• 36 min read • 7129 words
Tags: Ma-Le
Categories: Machine Learning

特征收缩方法

1. 岭回归

a.a. 简介

岭回归 (Ridge Regression) 是标准最小二乘法线性回归的一种改良版，它额外增加一个 ℓ2\ell_2 惩罚项。

岭回归的成本函数如下：

J(w)=∥Xw−y∥2+λ∥w∥2J(w) = \|Xw − y \|^2 + λ \|w\|^2

岭回归的正规方程如下：

(XTX+λI′)w=XTy\bigl(X^{T}X+\lambda I^{\prime}\bigr)w = X^{T}y

具体的数学推导在 “机器学习基础” 中已经讲解的非常详细了，这里略过。我们主要讲解 ℓ2\ell_2 惩罚项的一些实际意义。

根据前面的“偏差——方差权衡”理论，当我们增大 λ\lambda 时：

  • 方差减小：模型变得更简单、更平滑，对训练数据的随机噪声不再那么敏感。
  • 偏差增大：由于对模型加了限制，它可能无法完全捕捉数据中真实的复杂关系，导致模型欠拟合的风险增加。

我们再从几何角度解释一下这个正则化项的作用原理：

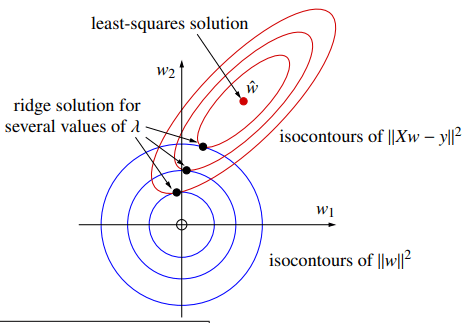
alt text

  • 红色椭圆：代表了误差项 ∥Xw−y∥2\|Xw − y\|^2 的等值线。椭圆的中心是普通最小二乘法的解 w^\hat{w}，这里是误差最小的地方。
  • 蓝色圆形：代表了惩罚项 ∥w∥2\|w\|^2 的等值线。圆心在原点，越靠近原点的圆代表权重越小。
  • 岭回归的解：岭回归的目标是最小化这两项之和。在几何上，这个解就是红色椭圆与蓝色圆形第一次相切的那个点。

由图像可以看出，λ\lambda 越大，惩罚越重，相当于对权重的限制越强。这会迫使解落在更小的蓝色圆上（更靠近原点），从而收缩 (shrink) 权重。

b.b. 基于最大后验概率的推导

下面我们基于最大后验概率来推导岭回归的正则化项（又称Tikhonov正则化）。

在贝叶斯公式中，有：

P(θ∣D)=P(D∣θ)P(θ)P(D)P(\theta|D) = \frac{P(D|\theta)P(\theta)}{P(D)}

其中 P(D∣θ)P(D|θ) 是似然 (Likelihood)，P(θ)P(\theta) 是先验 (Prior)。P(D)P(D) 是证据 (Evidence)，是数据的边际概率。在优化过程中，P(D)P(D) 是一个和 θθ 无关的常数。因此，我们希望最大化：

argmax⁡θ P(θ∣D)⇒argmax⁡θ [P(D∣θ)P(θ)]\underset{\theta}{\operatorname{argmax}}\, P(\theta |D) \Rightarrow \underset{\theta}{\operatorname{argmax}}\,[P(D|θ) P(θ)]

对这个式子取对数：

argmax⁡θ ln⁡(P(D∣θ)P(θ))=argmax⁡θ [ln⁡P(D∣θ)+ln⁡P(θ)]\underset{\theta}{\operatorname{argmax}}\,\ln\big(P(D|\theta)P(\theta)\big) = \underset{\theta}{\operatorname{argmax}}\,\big[\ln P(D|\theta)+\ln P(\theta)\big]

对于对数似然部分，我们前面推导过，在线性回归和高斯噪声的假设下，最大化它就等价于最小化残差平方和：

ln⁡P(D∣θ)=ln⁡∏i=1nP(yi∣xi,θ)=∑i=1nln⁡(1σn2πexp⁡(−(yi−xiTθ)22σn2))=∑i=1n(−ln⁡(σn2π)−(yi−xiTθ)22σn2)=−nln⁡(σn2π)−12σn2∑i=1n(yi−xiTθ)2\begin{aligned} \ln P(D|\theta) &= \ln \prod_{i=1}^n P(y_i|x_i, \theta) \\ &= \sum_{i=1}^n \ln \left( \frac{1}{\sigma_n\sqrt{2\pi}}\exp\left(-\frac{(y_i-x_i^T\theta)^2}{2\sigma_n^2}\right) \right) \\ &= \sum_{i=1}^n \left( -\ln(\sigma_n\sqrt{2\pi}) - \frac{(y_i-x_i^T\theta)^2}{2\sigma_n^2} \right) \\ &= -n\ln(\sigma_n\sqrt{2\pi}) - \frac{1}{2\sigma_n^2}\sum_{i=1}^n(y_i-x_i^T\theta)^2 \end{aligned}

于是问题转变为：我们应该对参数 θ\theta 做一个什么样的先验假设呢？一个合理的假设是：我们相信模型的参数 θθ 不会太大，它们的值应该倾向于靠近 0。因为一个参数值很小的模型通常更简单、更平滑，不容易过拟合。均值为 0 的高斯分布可以很好地满足我们的需求。

于是我们假设 θ∼N(0,σ2)\theta \sim \mathcal{N}(0, \sigma^2)，则：

ln⁡P(θ)=ln⁡∏j=1dP(θj)=∑j=1dln⁡(1σp2πexp⁡(−θj22σp2))=∑j=1d(−ln⁡(σp2π)−θj22σp2)=−dln⁡(σp2π)−12σp2∑j=1dθj2=−dln⁡(σp2π)−∥θ∥222σp2\begin{aligned} \ln P(\theta) &= \ln \prod_{j=1}^d P(\theta_j) \\ &= \sum_{j=1}^d \ln \left( \frac{1}{\sigma_p\sqrt{2\pi}}\exp\left(-\frac{\theta_j^2}{2\sigma_p^2}\right) \right) \\ &= \sum_{j=1}^d \left( -\ln(\sigma_p\sqrt{2\pi}) - \frac{\theta_j^2}{2\sigma_p^2} \right) \\ &= -d\ln(\sigma_p\sqrt{2\pi}) - \frac{1}{2\sigma_p^2}\sum_{j=1}^d\theta_j^2 \\ &= -d\ln(\sigma_p\sqrt{2\pi}) - \frac{\|\theta\|_2^2}{2\sigma_p^2} \end{aligned}

将上述两项代入 MAP 目标函数：

θ^MAP=argmax⁡θ [−nln⁡(σn2π)−12σn2∑i=1n(yi−xiTθ)2−dln⁡(σp2π)−∥θ∥222σp2]\hat{\theta}_{\text{MAP}} = \underset{\theta}{\operatorname{argmax}}\,\left[ -n\ln(\sigma_n\sqrt{2\pi}) - \frac{1}{2\sigma_n^2}\sum_{i=1}^n(y_i-x_i^T\theta)^2 -d\ln(\sigma_p\sqrt{2\pi}) - \frac{\|\theta\|_2^2}{2\sigma_p^2} \right]

在优化过程中，我们忽略所有与 θ\theta 无关的常数项：

θ^MAP=argmax⁡θ [−12σn2∑i=1n(yi−xiTθ)2−12σp2∥θ∥22]\hat{\theta}_{\text{MAP}} = \underset{\theta}{\operatorname{argmax}}\,\left[ - \frac{1}{2\sigma_n^2}\sum_{i=1}^n(y_i-x_i^T\theta)^2 - \frac{1}{2\sigma_p^2}\|\theta\|_2^2 \right]

令 λ=σn2σp2\lambda = \frac{\sigma_n^2}{\sigma_p^2}，我们就得到了岭回归 (Ridge Regression) 的目标函数：

θ^MAP=argmin⁡θ [∑i=1n(yi−xiTθ)2+λ∥θ∥22]\hat{\theta}_{\text{MAP}} = \underset{\theta}{\operatorname{argmin}}\,\left[ \sum_{i=1}^n(y_i-x_i^T\theta)^2 + \lambda\|\theta\|_2^2 \right]

2. 特征子集选择

该部分由 gemini 生成

在介绍 LASSO 之前，我们先简单介绍一下特征子集选择。

特征选择的基本思想很简单：并非所有特征都是有用的。在一个数据集中，很多特征可能与预测目标无关，或者包含了冗余信息。同时，使用重要的特征能够增强模型的可解释性：一个只用了5个最重要特征的模型，远比一个用了500个特征的“黑箱”模型更容易理解和解释。

最直接的方法是直接尝试所有的特征组合。对于 dd 个特征，总共有 2d−12^d-1 个不同的选择，这个数量级过于庞大了，因此我们一般采用启发式方法：

  • 算法 1：前向逐步选择 (Forward Stepwise Selection)
    • 方法：
      1. 从一个不包含任何特征的“空模型”开始。
      2. 遍历所有尚未被选入的特征，将它们逐一加入当前模型，看哪个能让模型的性能提升最大（例如，通过交叉验证评估）。
      3. 将这个“最佳”特征正式加入模型。
      4. 重复步骤2和3，直到模型性能不再提升为止。
    • 缺点：它是一种贪心算法，可能会错过最优解。例如，最好的特征对 {A,B}\lbrace A, B \rbrace 可能无法被找到，因为单独的 AA 和单独的 BB 都不是最好的单特征模型。
  • 算法 2：后向逐步选择 (Backward Stepwise Selection)
    • 方法：
      1. 从包含所有 d 个特征的“全模型”开始。
      2. 遍历所有已在模型中的特征，尝试逐一移除它们，看移除哪个能让模型的性能提升最大。
      3. 正式移除这个“最没用”的特征。
      4. 重复步骤2和3，直到模型性能不再提升为止。

这些算法的适用场景如下：

  • 前向选择更适合只有少数特征是真正有用的场景。
  • 后向选择更适合大部分特征都有用，只有少数是无用的场景。

3. LASSO 方法

LASSO ((Least Absolute Shrinkage and Selection Operator)) 全称是“最小绝对值收缩和选择算子”，它是一种非常巧妙的正则化方法。

与岭回归不同，LASSO 使用如下的正则化方法：

J(w)=∥Xw−y∥2+λ∑∣wi∣J(w) = \|Xw − y\|^2 + λ \sum|w_i|

正是从平方和到绝对值和这个微笑的改动，使得 LASSO 能够自然地将某些特征的权重精确地压缩到 0，从而自动进行特征选择。

为了理解 LASSO 的特征选择，我们从几何角度作出它的图像：

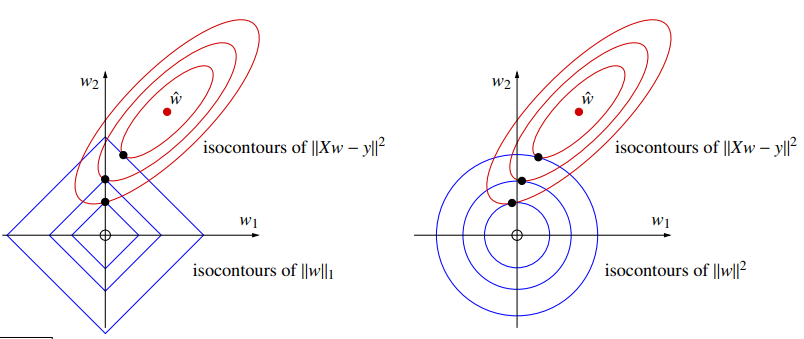
alt text

LASSO 的 L1L_1 惩罚项的等值线是菱形，当误差等值线从中心点（最小二乘解）向外扩张时，它有极大的概率首先碰到菱形的一个顶点，而不是一条边。而菱形的顶点正好位于坐标轴上，例如，如果切点在 w2w_2 轴的顶点上，那么该点的 w1w_1 坐标就精确地为 0。这就是 LASSO 能够进行特征选择的几何原理。通过使用 L1L_1 惩罚，它创造了带有“尖角”的约束区域，使得最优解天然地倾向于落在这些角上，从而导致某些权重变为零。

LASSO 的权重路径图如下：

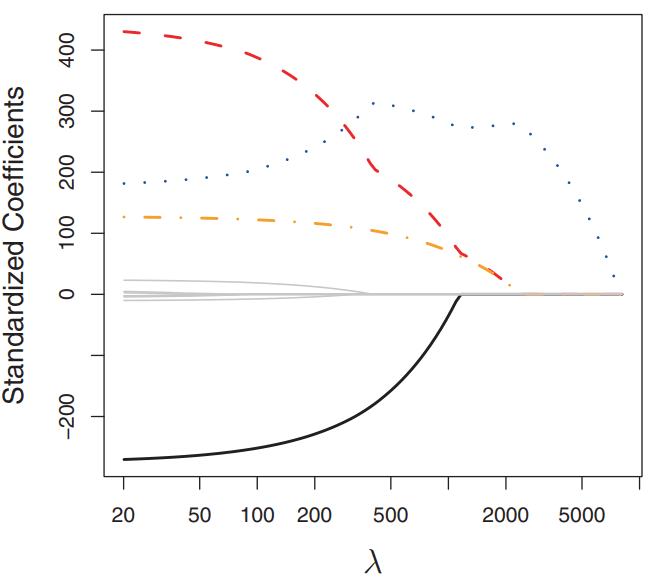
alt text

可以清晰地看到，随着 λ\lambda 从左到右增大，一条又一条的权重曲线被压到了 0，并且保持为 0。

在实际使用LASSO 方法时需要注意如下的事项：

  • LASSO 没有像岭回归那样的解析解，需要使用专门的优化算法来求解。
  • 与岭回归一样，在使用 LASSO 之前，强烈建议先对特征进行标准化（例如，将它们缩放到均值为0，方差为1）。这是因为 LASSO 的惩罚是基于权重的绝对值，如果特征的尺度相差很大，那么尺度大的特征对应的权重会天然地更小，惩罚对它们就不公平了。

Comments

Total words: 7129