软边界分类器

我们之前讲的最大间隔分类器有如下的弊端：

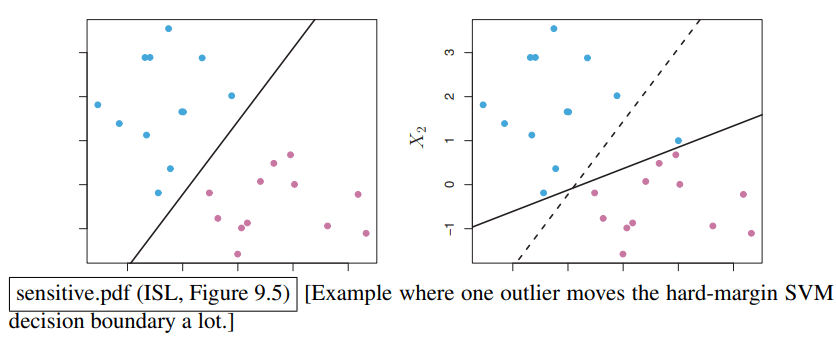
alt text

我们只是添加了一个离群值，但是得到的最大间隔划分却发生了很大变化。虽然这个划分仍然是正确的，但是间隔的宽度变小了很多，这导致分类器的鲁棒性大大下降。

为了解决这些问题，我们引入特征映射和软间隔分类器（Soft-Margin Classifier）两个工具。

特征映射是处理非线性问题的常用手段。

对非线性问题，一个直观的想法是：在低维空间中看起来线性不可分的数据，在映射到一个足够高的维度空间后，可能就变得线性可分了。在这个高维空间中，我们就可以使用已有的线性分类器了。这个过程就是特征映射。

以下面这个图片为例：

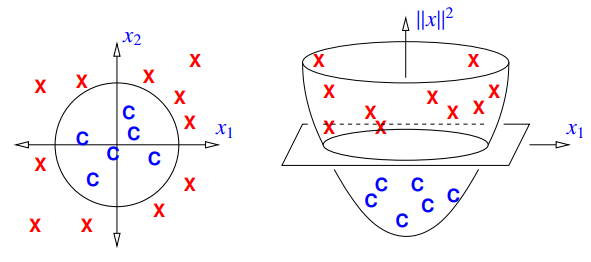
alt text

我们定义如下的特征映射

\Phi(x):\mathbb{R}^d\rightarrow\mathbb{R}^{d+1},\Phi(x)=\begin{bmatrix} x \\ \|x\|_2 \end{bmatrix}

这个特征映射给我们提供了一个新的特征，这个特征将二维向量 $x$ 映射到了三维空间中。此时的 SVM 就可以使用圆形作为决策边界、而不是单纯的直线了。

这里有一个简单的定理：当且仅当 $(x_1, ..., x_n)$ 可通过超球实现可分时， $Φ(x_1), ..., Φ(x_n)$ 是线性可分的。证明如下：

\begin{aligned} \Rightarrow\;& \|x-c\|_2^2 < \rho^2 \\[4pt] \Rightarrow\;& \|x\|_2^2 - 2\,c\cdot x + \|c\|_2^2 < \rho^2 \\[6pt] \Rightarrow\;& [-2\,c^\top\ \ 1]\, \begin{bmatrix} x \\ \|x\|_2^2 \end{bmatrix} < \rho^2 - \|c\|_2^2 \\[6pt] \Rightarrow\;& \text{normal vector in }\mathbb{R}^{d+1}:\ [-2\,c^\top\ \ 1],\qquad \Phi(x)=\begin{bmatrix} x \\ \|x\|_2^2 \end{bmatrix} \end{aligned}

进一步，我们还可以引入交叉项：

Φ(x) = [x₁, x₂, x₃, x₁², x₂², x₃², x₁x₂, x₂x₃, x₃x₁]^T

在这个高维空间中应用线性分类器，其决策边界投影回原始的三维空间时，会变成各种各样的二次曲面 (Quadric)，比如任意方向的椭球、双曲面、抛物面等。这使得决策边界的形状变得极其灵活。

虽然特征映射方法非常强大，但是如果原始维度为 $d$ ，那么二次交叉项的数量级为 $d^2$ ，所有的多项式项的数量级为 $d^n$ ，这很容易导致维度爆炸的问题。

为了减轻少部分离群值对线性分类器的影响，我们可以通过允许少数几个点犯错（如被错误分类，或者进入间隔带），来换取一个对整体数据而言更宽、更鲁棒的分类边界。这正是软间隔分类器的思想。

我们为每一个数据点 $i$ 引入一个松弛变量 $\xi _i \ge 0$ 。我们的间隔约束变为：

y_i(X_i \cdot w + \alpha) \ge 1 - \xi_i,

$\xi_i$ 的实际含义如下：

$\xi_i = 0$ ：约束变为原来的 $y_i(X_i \cdot w + \alpha) \ge 1$ ，说明这个点符合原先的硬间隔分类器约束、没有超出边界。
$0 \lt \xi_i \le 1$ ：这个点违反了间隔，进入了间隔带，但它仍然在决策边界正确的一侧。
$\xi_i \ge 1$ ：这个点被彻底错误分类了。

$\frac{\xi_i}{\|w\|}$ 表示了该点越过边界的实际距离。

引入 $\xi_i$ 后，我们的优化目标也变为了在“最大化间隔”和“最小化犯错”之间权衡，我们引入超参数 $C$ ，则我们的目标为：

\min \|w\|^2 + C \sum_{i=1}^n \xi_i,\quad i=1,\dots,n

当 $C$ 很大时，模型的行为倾向于硬间隔分类器，导致间隔变窄；当 $C$ 很小时，模型的行为倾向于扩大间隔宽度，它会忽略更多的离群点，不过如果 $C$ 值过小，会导致欠拟合的问题。