生成：Gemini-2.5-pro， 整理：fyerfyer

迁移学习

2. 适配器 (Adapters)

为了解决传统微调的参数效率问题，论文提出了一种替代方案，叫做适配器模块 (Adapter Modules)。

a. 核心思想

适配器的核心思想是：在为下游任务调整模型时，我们完全冻结 (freeze) 预训练模型的全部参数，然后在其网络层之间插入一些新的、小型的、可训练的模块（即“适配器”）。在训练时，只有这些适配器模块的参数会被更新。

这种方法具备三个关键特性：

1. 性能好：最终效果接近传统的完全微调方法。在GLUE基准上，适配器方法的性能仅比“完全微调”低了0.4%，但每个任务只增加了3.6%的参数。
2. 可串行训练：无需同时访问所有任务的数据集，可以一个任务接着一个任务地进行训练，并且不会忘记旧任务（完美解决“灾难性遗忘”）。
3. 参数增量小：每个新任务只增加极少的模型参数，实现了极高程度的参数共享。

b. 适配器的工作原理

适配器可以看作是一种函数组合。它通过向原始网络 $f_w(x)$ 中注入新的、针对特定任务的函数 $\psi_{v}(x)$ 来重新调整模型的功能。

其中，原始模型的参数 $w$ 被冻结，只有为新任务添加的适配器参数 $v$ 会被训练。

i. 瓶颈结构 (Bottleneck Architecture)

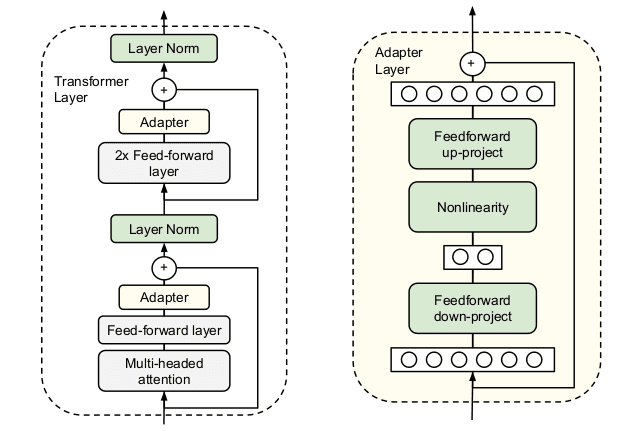
为了实现“参数量小”这一目标，适配器模块采用了一种“瓶颈”结构，它由两个前馈神经网络层和一个非线性激活函数组成：

1. 降维 (Down-projection)：首先，一个全连接层将原始的 $d$ 维特征投影（压缩）到一个更小的维度 $m$。
2. 非线性激活：然后，应用一个非线性激活函数（如ReLU）。
3. 升维 (Up-projection)：最后，再通过另一个全连接层，将 $m$ 维特征投影回原始的 $d$ 维。

因为 $m \ll d$，所以这个结构极大地限制了每个任务需要增加的参数量。每一层增加的总参数量为 $2md + d + m$。

ii. 残差连接与近似恒等初始化

适配器模块自身内部包含一个残差连接 (skip-connection)。这使得适配器的输出等于其内部变换的输出与原始输入的加和：

这个设计非常巧妙，它使得“近似恒等初始化 (near-identity initialization)” 成为可能：

• 在训练开始时，我们将 $W_{down}$ 和 $W_{up}$ 的权重初始化为接近零的数值。
• 这样，在初始阶段，$W_{up}(\sigma(W_{down}x))$ 的输出也接近于零。
• 因此，整个适配器模块的输出就约等于通过残差连接直接传过来的输入 $x$。

这保证了在训练刚开始时，适配器模块像一个“透明”的层，不会破坏预训练模型强大的初始能力，从而保证了训练的稳定性。

iii. 在Transformer中的应用

在Transformer架构中，适配器被插入到每个核心块的子层之后。具体来说，在每个Transformer层中：

1. 在多头注意力层 (Multi-head Attention) 之后，但在残差连接被加回来之前，插入一个适配器。
2. 在前馈网络层 (Feed-Forward Network) 之后，但在残差连接被加回来之前，再插入一个适配器。

适配器的输出会直接进入后续的层归一化（Layer Normalization）。

3. 核心概念：残差连接与层归一化

残差连接 (Residual Connection) 和 层归一化 (Layer Normalization) 是构建像Transformer这样的深度网络的基石。

a. 残差连接 (Residual Connection)

• 问题：解决了深度网络的“退化”问题。即当网络过深时，性能反而下降，因为让多层非线性网络学习一个简单的恒等映射（即什么都不做，直接传递输入）都非常困难。
• 原理：我们不直接学习目标输出 $H(x)$，而是学习它与输入 $x$ 之间的差值，即残差 $F(x) = H(x) - x$。通过一条“近道”将输入 $x$ 直接加到网络块的输出上，最终得到 $F(x) + x$。
• 效果：如果某个网络块是多余的，模型只需将 $F(x)$ 的权重学成0，就能轻松实现恒等映射。这极大地缓解了梯度消失问题，使得构建上百层的网络成为可能。

b. 层归一化 (Layer Normalization)

• 问题：解决了“内部协变量偏移”问题。即在训练中，前层参数的更新导致后层输入的数据分布剧烈变化，使得训练不稳定。
• 原理：它在单个样本的层级上，对该样本的所有特征（一个向量）进行归一化。
  1. 计算该样本特征向量的均值和方差。
  2. 用每个元素减去均值、除以标准差，得到一个均值为0、方差为1的新向量。
  3. 通过两个可学习的参数 $\gamma$ (缩放) 和 $\beta$ (偏移) 对归一化后的向量进行调整，以恢复模型的表达能力。
• 与批归一化(Batch Norm)的区别：批归一化是在一个批次(batch)的所有样本中，对同一个特征进行归一化。层归一化是在一个样本中，对所有特征进行归一化。这使得它特别适合处理文本等变长序列数据。