无监督学习

与前面的训练不同，无监督学习只有样本点而没有标签。它的核心目标是在没有外部指导的情况下，发现数据本身固有的结构、模式或关系。

1. 主成分分析

$a.$ 概述

主成分分析 (Principal Components Analysis, PCA) 的目标是：在一个 $d$ 维的数据空间中，找到 $k$ 个新的坐标轴（方向），这些新的坐标轴能够捕捉到数据中最大部分的变异性（variation）。换句话说，就是找到最能“概括”数据分布的方向。

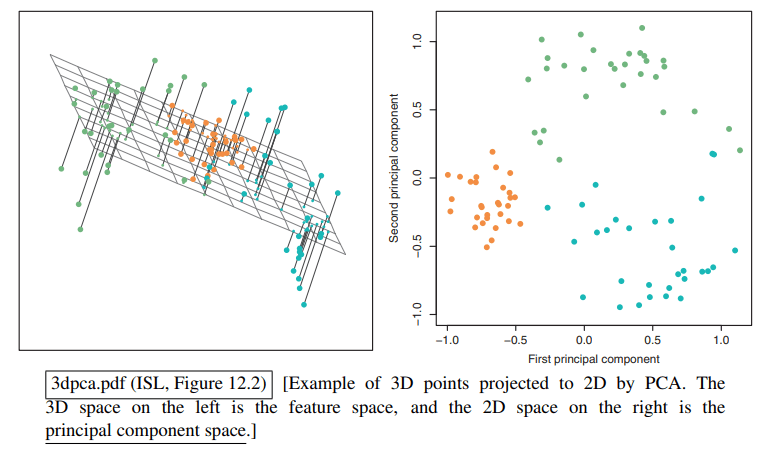
alt text

PCA 可以降低模型的维度，从而降低计算成本。同时维度特征的减少也可以减少过拟合，让模型更关注核心特征，从而提高泛化能力。

这类似于特征选择，但 PCA 找到的新特征是原始特征的线性组合，而不是简单地从原始特征中挑选。

$b.$ 算法

假设我们的数据是一个 $n\times d$ 的矩阵 $X$ 。

首先，我们对数据进行数据中心化：我们计算所有样本的平均值，然后让每个样本点都减去这个平均值。这样，现在的数据表示的是相对于平均值的偏差。

然后我们引入投影 (Projection) 的概念，向量 $x$ 在方向向量 $w$ 上的投影为 $\tilde{x}=(x\cdot w)w$ 。PCA 的目标就是找到最好的投影方向 $w$ ，使得数据在该方向上的分布最为分散（也即方差最大）。下面我们进行推导。

我们将整个数据矩阵投影到 $w$ 上：

\tilde{X}=Xw

因为 $X$ 的均值为 0 (因为已经中心化了)，则 $\tilde{X}$ 的均值也为 0，因此我们需要最大化的方差为：

\sigma^2=\frac{1}{n}(Xw)^T(Xw)=\frac{1}{n}w^TX^TXw

我们令 $S=X^TX$ ，则问题转变为最大化 $w^TSw$ 。这是一个在数学和物理中非常经典的问题。线性代数中有一个著名的定理（Rayleigh Quotient）告诉我们：对于一个对称矩阵 $S$ ，表达式 $w^TSw$ 的最大值，会在 $w$ 是该矩阵最大特征值 $λ_{max}$ 所对应的特征向量时取到，并且最大值本身就是 $λ_{max}$ 。

因此，数据的第一主成分就是 $X^TX$ 的最大特征向量，第二主成分为次大的特征向量，以此类推。

我们可以根据累积方差贡献率来决定选择多少个主成分，如选择 $k$ 个主成分，使得它们能解释总方差的 95%。

在得到这些主成分后，我们将原始数据点投影到这些主成分上，得到新的 $k$ 维坐标 $x \cdot v_i$ ，主成分分析就完成了。

2. 奇异值分解

$a.$ PCA 算法的问题

在 PCA 中，我们需要计算矩阵 $X^TX$ ，这个计算的时间复杂度是 $\Theta(nd^2)$ 。当特征维度 $d$ 很大时，这个计算量非常巨大。

同时，计算出的 $X^T X$ 矩阵可能是一个“病态矩阵”：矩阵的条件数（最大特征值与最小特征值之比）非常大。对于这样的矩阵，计算其特征向量时，微小的计算误差都可能被急剧放大，导致最终结果不准确。而我们计算主成分的方法 $X^TX$ 会进一步放大这个误差：

\kappa\!\left(X^{T}X\right) \;=\; \left[\kappa(X)\right]^{2}

为了解决这个问题，可以用 SVD 来寻找 PCA 所需的主成分。

$b.$ 数学推导

由于要获取特征值，我们对 $X^TX$ 进行特征分解。对于一个方阵 $A$ ，它的特征值分解被定义为：

A = P \Lambda P^{-1}

其中：

$P$ 是一个矩阵，它的列向量是 $A$ 的特征向量。 $\Lambda$ 是一个对角矩阵，它的对角线元素是 A 对应的特征值。

这里的推导可以参见“特征值分解”一章的笔记。

于是我们先得到了标准的分解形式，之后我们会将推导出的式子和这个进行比对：

X^T X = P \Lambda P^T

现在我们使用奇异值分解 (SVD)：任何一个 $n x d$ 维的矩阵 $X$ 都可以被分解为三个矩阵的乘积：

X = U D V^T

其中U 是一个 $m x m$ 的正交矩阵， $D$ 是一个 $m x n$ 的对角矩阵， $V^T$ 是一个 $n x n$ 的正交矩阵 $V$ 的转置。

关于 SVD 分解的详细讲解可以参照我之前的笔记。

alt text

将 SVD 分解的结果代入：

\begin{aligned} X^{T}X &= (U\,D\,V^{T})^{T}\,(U\,D\,V^{T})\\[6pt] &= \bigl(V\,D^{T}\,U^{T}\bigr)\,\bigl(U\,D\,V^{T}\bigr) \end{aligned}

因为 $U$ 是标准正交的， $U^T U = I$ ，则：

X^T X = V (D^T D) V^T

这正是前面标准的特征值分解形式，其中：

$V$ 是 $X^T X$ 的特征向量矩阵。
$D^T D$ 是 $X^T X$ 的特征值对角矩阵，其对角线上的元素就是 $\delta_i^2$ 。

SVD 分解相对于 PCA 更稳定：奇异值的比率 $\delta_{max} / \delta_{min}$ 通常远小于特征值的比率 $\delta_{max}^2 / \delta_{min}^2$ 。在数值计算中，处理差异没那么悬殊的数字会更稳定、更精确。

$c.$ 主坐标

推导完使用 SVD 的 PCA 后，我们再来看看将 $X$ 沿主坐标投影会发生什么。由前面的分解：

\begin{aligned} X\,V &= (UDV^{T})\,V\\[6pt] &= UD(V^{T}V)\\[6pt] &= UD \end{aligned}

可以看到，矩阵 $UD$ 的第 $i$ 行，直接给出了原始数据点 $X_i$ 的主坐标。

$d.$ 紧凑 SVD

在实际应用中，很多奇异值可能是0（或者非常接近0）。这些奇异值为0的成分对于重构矩阵 $X$ 没有任何贡献。因此，我们可以把它们丢掉，这就引出了紧凑SVD。

假设矩阵 $X$ 的秩为 $r$ ，这意味着它只有 $r$ 个非零的奇异值，我们可以做如下的紧凑 SVD：

X = U_r(n×r) D_r(r×r) V_r^T(r×d)

这样可以节省存储与运算空间。

3. 聚类

$a.$ 概述

聚类是一种无监督学习方法，它的目标是将数据集中的样本划分成若干个簇（cluster）：同一个簇内的数据点彼此之间非常相似，而不同簇之间的数据点则差异很大。

聚类主要有如下的应用场景：

探索数据特征，寻找隐藏的模式或群体，在网络结构中寻找社群。
构建事物的分类体系。
进行数据压缩，将数据中的很多点都使用所属簇的中心点来表达。

$b.$ k-means

k-means 的目标是将 $n$ 个数据点划分到 $k$ 个互不相交的簇中。我们定义：

$X_i$ : 第 $i$ 个数据点。
$y_i$ : 数据点 $X_i$ 所属的簇的标签。
$\mu_i$ : 第 $i$ 个簇的均值或中心点 (mean/centroid)，为该簇内所有数据点的算术平均值。
$n_i$ : 第 $i$ 个簇中数据点的数量。

算法的目标是找到一个最优的簇分配方案 $y$ ，使得所有数据点到其所属簇中心点的平方距离之和 (Sum of Squared Errors, SSE) 最小：

\begin{aligned} \min_{\{\mu_i\}_{i=1}^{k}} \;&=\; \sum_{i=1}^{k}\sum_{X_j\in C_i}\left\|X_j-\mu_i\right\|^{2} \end{aligned}

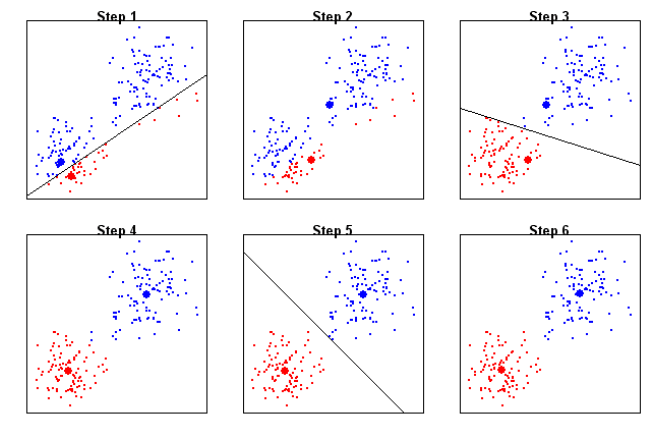
这是一个 NP-hard 问题，如果想找到全局最优解，理论上需要尝试所有可能的划分方式，时间复杂度高达 $O(n^k)$ 。为此， k-means 采用了一种启发式策略：我们交替进行下面的步骤：

更新均值：固定 $y_i$ 计算每个簇的中心点 $\mu_i$ 。
更新分配：固定每个簇的中心点 $\mu_i$ $μ_{i}$ ，将每个数据点 $X_j$ $X_{j}$ 重新分配给离它最近的那个簇中心点 $\mu_i$ 所代表的簇。
- 如果出现距离相等的情况，并且其中一个选项是保持上一次迭代的分配不变，那么就选择保持不变，这有助于算法稳定。

算法在这两个步骤之间不断迭代，直到步骤二不再改变任何数据点的簇分配时，算法收敛并停止。

alt text

在 k-means 算法中，初始中心点的选择对最终结果影响很大。常见的初始化方法有：

Forgy 方法: 随机从数据集中选择 $k$ 个点作为初始的簇中心点 $\mu_i$ ，然后直接开始更新分配。
随机划分: 将每个数据点随机分配到一个簇，然后开始更新均值。
k-means++: 这是目前最推荐的方法。它也随机选择初始点，但带有一定的策略：下一个初始中心点的选择会优先考虑那些离已选中心点较远的点。这使得初始中心点能更均匀地散布在数据空间中，从而更容易找到一个好的局部最优解。

下面是 k-means++ 的完整实现，唯一比较麻烦的地方是二阶范数的计算：

def kmeans_pp_nn(X, center_index_0, k, j):
    n_samples, n_features = X.shape
    centers_indices = [center_index_0]

    for _ in range(1, k):
        current_center = X[centers_indices]
        D = -2 * X @ current_center.T + (X ** 2).sum(axis=1)[:, None] + (current_center ** 2).sum(axis=1)
        # Compute the distances of all remaining points to all selected centers
        distances = np.min(D, axis=1)

        # Sort the list of data points (in decreasing order) by the minimum such distance
        sorted_indices = np.argsort(distances)[::-1]

        # Choose the jth element of the list in this sorted order as the next center
        next_center_index = sorted_indices[j]
        centers_indices.append(next_center_index)

    return centers_indices

$c.$ 层次聚类

$i.$ 聚类思想

与k-means将数据划分成k个独立的簇不同，层次聚类会创建一个树状的结构（通常是二叉树），这棵树被称为树状图 (Dendrogram)。在这棵树中，每一个子树都代表一个簇：

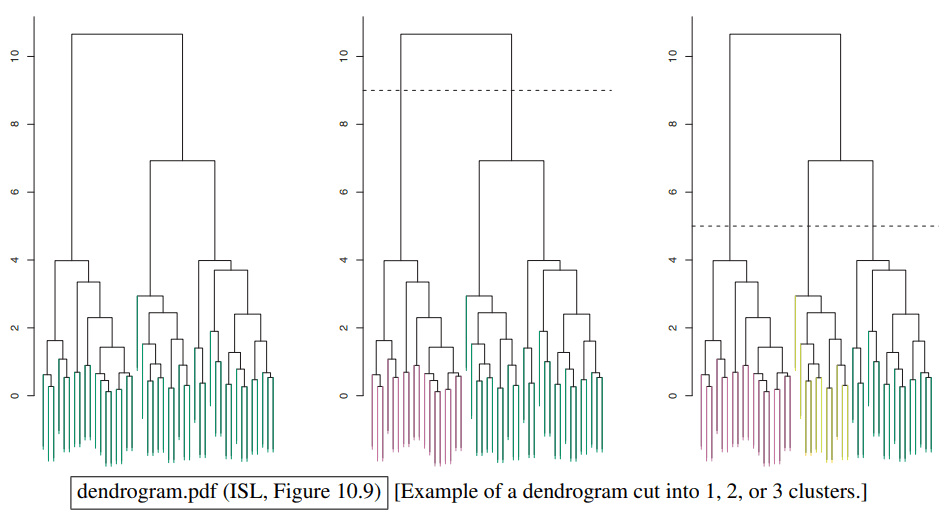
alt text

层次聚类主要有两种方法：

自底向上 (Bottom-up)，也称为凝聚式聚类 (agglomerative clustering)：开始时，每个数据点都自成一簇。然后，算法会重复地将最相似（距离最近）的两个簇合并成一个新簇。这个过程不断重复，直到所有数据点都合并到同一个根簇中。
自顶向下 (Top-down)，也称为分裂式聚类 (divisive clustering)：开始时，所有数据点都在一个大簇中。然后，算法重复地将一个簇分裂成两个最不相似的子簇。这个过程不断重复，直到每个点都自成一簇，或者达到了预设的簇数量。
- 当输入是点集时，凝聚式聚类用得远比分裂式聚类多。但当输入是图时，分裂式聚类（如图分割算法）更常见。

$b.$ 划分方法

对于凝聚式聚类，关键问题是如何衡量两个簇 $A$ 和 $B$ 之间的距离 $d(A, B)$ 。这由连接方法 (Linkage) 来定义。有如下的连接方法：

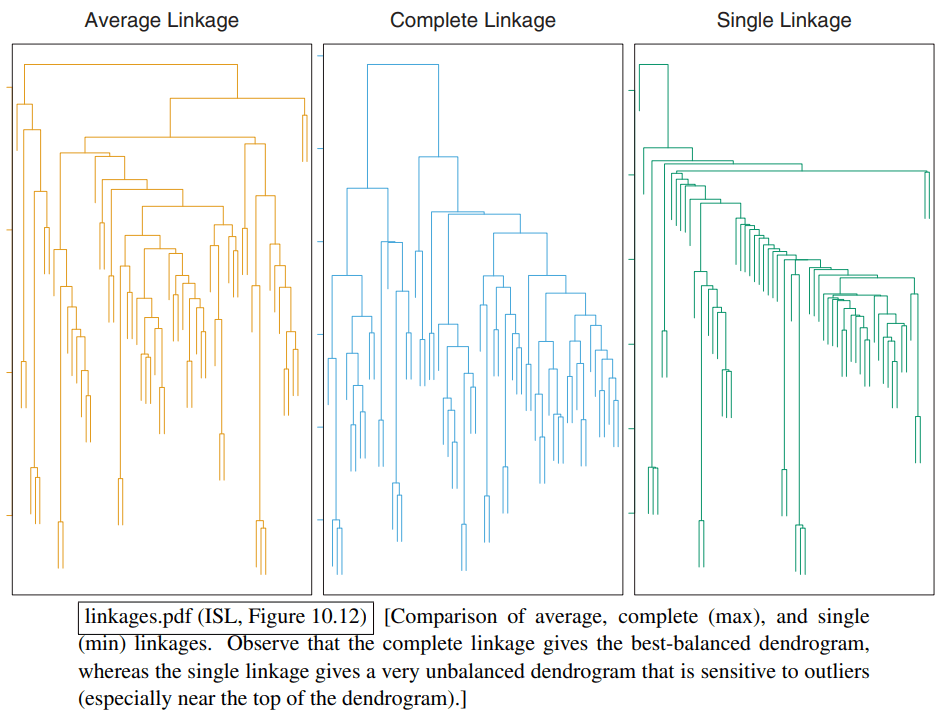
完全连接 (complete linkage) 将距离定义为两个簇中最远的两个点之间的距离。只有当 $A$ $A$ 中所有点都和 $B$ $B$ 中所有点靠得足够近时，这两个簇的距离才近。
- 它倾向于产生最平衡的簇。因为它要求一个簇中所有点都和另一个簇中所有点离得近才能合并。当一个簇变大时，它内部最远的点会离其他簇很远，因此大簇更难继续“生长”。

d(A, B) = \max \lbrace d(w, x) : w \in A, x \in B \rbrace

单一连接 (single linkage)将距离定义为两个簇中最近的两个点之间的距离。只要 $A$ $A$ 中有一个点和 $B$ $B$ 中有一个点离得近，这两个簇的距离就近。
- 这种连接方式对异常值非常敏感。两个簇只要有一对点离得近，就可能被合并，这容易导致“链式效应”：即一个簇通过一系列中间点不断地“吞并”远处的点，形成一个长链状、不紧凑的簇。这也会导致树的不平衡。

d(A, B) = min{d(w, x) : w ∈ A, x ∈ B}

平均连接 (average linkage) 将距离定义为两个簇中所有点对之间距离的平均值。它综合考虑了所有点的信息：
- 它是一种介于单一连接和完全连接之间的折中方案，表现通常比较稳健。

d(A, B) = (1 / |A||B|) * Σ(w∈A) Σ(x∈B) d(w, x)

中心点连接 (centroid linkage) 将距离定义为两个簇的中心点之间的距离。：

d(A, B) = d(µA, µB)

完全、单一、平均连接方法适用于任何距离函数 $d(w, x)$ ，但中心点连接只有在使用欧几里得距离时才有明确的物理意义，因为“中心点”的概念通常是基于欧氏空间中的均值来计算的。

alt text

对于凝聚式层次聚类，我们通常使用贪心凝聚算法，流程如下：

将每个点初始化为一个簇。
重复以下步骤，直到只剩一个簇：
- 在当前所有的簇中，找到距离 $d(A, B)$ 最小的那一对簇。
- 将这两个簇合并成一个新簇。

注意，到目前为止我们研究的所有聚类算法都是不稳定的：从数据集中删除或微调少数几个样本点，有时可能会导致聚类结果发生巨大变化。

无监督学习

1. 主成分分析

a.a.a. 概述

b.b.b. 算法

2. 奇异值分解

a.a.a. PCA 算法的问题

b.b.b. 数学推导

c.c.c. 主坐标

d.d.d. 紧凑 SVD

3. 聚类

a.a.a. 概述

b.b.b. k-means

c.c.c. 层次聚类

i.i.i. 聚类思想

b.b.b. 划分方法

Comments

$a.$ 概述

$b.$ 算法

$a.$ PCA 算法的问题

$b.$ 数学推导

$c.$ 主坐标

$d.$ 紧凑 SVD

$a.$ 概述

$b.$ k-means

$c.$ 层次聚类

$i.$ 聚类思想

$b.$ 划分方法